【题目】某班“2016年联欢会”中,有一个摸奖游戏:有4张纸牌,背面都是喜羊羊头像,正面有2张是笑脸,2张是哭脸,现将4张纸牌洗匀后背面朝上摆放到桌上,然后让同学去翻纸牌.
(1)现在小芳和小霞分别有一次翻牌机会,若正面是笑脸,则小芳获奖;若正面是哭脸,则小霞获奖,她们获奖的机会相同吗?判断并说明理由.
(2)如果小芳、小明都有翻两张牌的机会.翻牌规则:小芳先翻一张,放回后再翻一张;小明同时翻开两张纸牌.他们翻开的两张纸牌中只要出现笑脸就获奖.请问他们获奖的机会相等吗?判断并说明理由.
参考答案:
【答案】(1)相同,理由见解析;(2)机会不相等,理由见解析.
【解析】试题分析:(1)因为有4张纸牌,背面都是喜羊羊头像,正面有2张笑脸、2张哭脸,翻一次牌正面是笑脸的就获奖,正面是哭脸的不获奖,所以她们获奖的概率都是![]() ,获奖的机会相同;(2)先列举出小芳和小明翻牌的所有情况,然后分别计算出她们获奖的概率,比较她们获奖的概率,若概率相等,那么她们的获奖机会相等,若概率不相等,那么她们获奖机会不相等.
,获奖的机会相同;(2)先列举出小芳和小明翻牌的所有情况,然后分别计算出她们获奖的概率,比较她们获奖的概率,若概率相等,那么她们的获奖机会相等,若概率不相等,那么她们获奖机会不相等.
试题解析:
(1)∵有4张纸牌,背面都是喜羊羊头像,正面有2张笑脸、2张哭脸,翻一次牌正面是笑脸的就获奖,正面是哭脸的不获奖,
∴她们获奖的概率都是![]() ,
,
∴她们获奖机会相同;
(2)他们获奖机会不相等,理由如下:
小芳:
第一张 第二张 | 笑1 | 笑2 | 哭1 | 哭2 |
笑1 | 笑1,笑1 | 笑2,笑1 | 哭1,笑1 | 哭2,笑1 |
笑2 | 笑1,笑2 | 笑2,笑2 | 哭1,笑2 | 哭2,笑2 |
哭1 | 笑1,哭1 | 笑2,哭1 | 哭1,哭1 | 哭2,哭1 |
哭2 | 笑1,哭2 | 笑2,哭2 | 哭1,哭2 | 哭2,哭2 |
∵共有16种等可能的结果,翻开的两张纸牌中只要出现笑脸的有12种情况,
∴P(小芳获奖)=![]() =
=![]() ;
;
小明:
第一张 第二张 | 笑1 | 笑2 | 哭1 | 哭2 |
笑1 | 笑2,笑1 | 哭1,笑1 | 哭2,笑1 | |
笑2 | 笑1,笑2 | 哭1,笑2 | 哭2,笑2 | |
哭1 | 笑1,哭1 | 笑2,哭1 | 哭2,哭1 | |
哭2 | 笑1,哭2 | 笑2,哭2 | 哭1,哭2 |
∵共有12种等可能的结果,翻开的两张纸牌中只要出现笑脸的有10种情况,
∴P(小明获奖)=![]() =
=![]() ,
,
∵P(小芳获奖)≠P(小明获奖),
∴他们获奖的机会不相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)试判断AB与AF,EB之间存在的数量关系,并说明理由.

-
科目: 来源: 题型:
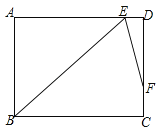
查看答案和解析>>【题目】在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC=____.(结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年4月22日是第
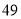 个世界地球日,今年的主题为“珍惜自然资源呵护美丽国土一讲好我们的地球故事”地球日活动周中,同学们开展了丰富多彩的学习活动,活动周期间,两位家长计划带领若干学生去参观山西地质博物馆,他们联系了两家旅行社,报价均为每人
个世界地球日,今年的主题为“珍惜自然资源呵护美丽国土一讲好我们的地球故事”地球日活动周中,同学们开展了丰富多彩的学习活动,活动周期间,两位家长计划带领若干学生去参观山西地质博物馆,他们联系了两家旅行社,报价均为每人 元.经协商,甲旅行社的优惠条件是,家长免费,学生都按九折收费.乙旅行社的优惠条件是,家长、学生都按八折收费.若只考虑收费,这两位家长应该选择哪家旅行社更合算?
元.经协商,甲旅行社的优惠条件是,家长免费,学生都按九折收费.乙旅行社的优惠条件是,家长、学生都按八折收费.若只考虑收费,这两位家长应该选择哪家旅行社更合算? -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料题
点A、B在数轴上分别表示实数
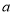 、
、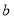 ,A、B两点之间的距离记作AB. 当A、B两点中有一点为原点时,不妨设A点在原点。如下图①所示,则AB =OB =
,A、B两点之间的距离记作AB. 当A、B两点中有一点为原点时,不妨设A点在原点。如下图①所示,则AB =OB =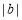 =
=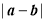 .
.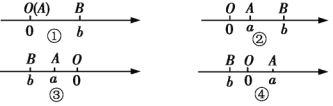
当A、B两点都不在原点时:
(1)上图②所示,点A、B都在原点的右边,不妨设点A在点B的左侧,则AB=OB-OA=
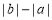 =
=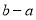 =
=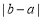 =
=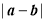
(2)上图③所示,点A、B都在原点的左边,不妨设点A在点B的右侧,则AB=OB-OA=
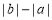 =
=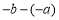 =
=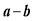 =
=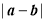
(3)如上图④所示,点A、B分别在原点的两边,不妨设点A在点O的右侧,则AB=OB+OA=
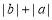 =
=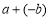 =
=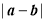
回答下列问题:
①综上所述,数轴上A、B两点之间的距离AB= .
②数轴上表示2和
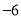 的两点A和B之间的距离AB= .
的两点A和B之间的距离AB= .③数轴上表示x和
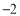 的两点A和B之间的距离AB= ,如果AB=2,则x的值为 .
的两点A和B之间的距离AB= ,如果AB=2,则x的值为 .④若代数式
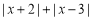 有最小值,则最小值为 .
有最小值,则最小值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】开学前,小强、小亮和小伟去文化用品商店购买笔和本,小强用17元买了1支笔和4个本,小亮用19元买了2支笔和3个本,小伟购买上述价格的笔和本共用了48元,且本的数量不少于笔的数量,则小伟的购买方案共有( )
A. 1种B. 2种C. 3种D. 4种
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘轮船以18海里/时的速度由西向东方向航行,行至A处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,求轮船与灯塔的最短距离.(精确到0.1,
 ≈1.73)
≈1.73)
相关试题

