【题目】某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的原始分均为![]() 分.前
分.前![]() 名选手的得分如下:根据规定,笔试成绩和面试成绩分别按一定的百分比折合成综合成绩(综合成绩的满分仍为
名选手的得分如下:根据规定,笔试成绩和面试成绩分别按一定的百分比折合成综合成绩(综合成绩的满分仍为![]() 分),现得知
分),现得知![]() 号选手的综合成绩为
号选手的综合成绩为![]() 分.
分.
序号 |
|
|
|
笔试成绩/分 |
|
|
|
面试成绩/分 |
|
|
|
(1)求笔试成绩和面试成绩各占的百分比:
(2)求出其余两名选手的综合成绩,并以综合成绩排序确定这三名选手的名次。
参考答案:
【答案】(1)笔试占![]() ,面试占
,面试占![]() ;(2)第一名:2号,第二名:1号,第三名:3号.
;(2)第一名:2号,第二名:1号,第三名:3号.
【解析】
(1)设笔试成绩占百分比为![]() ,则面试成绩占比为
,则面试成绩占比为![]() ,根据题意列出方程,求解即可;
,根据题意列出方程,求解即可;
(2)根据笔试成绩和面试成绩各占的百分比,分别求出其余两名选手的综合成绩,即可得出答案.
解:(1)设笔试成绩占百分比为![]() ,则面试成绩占比为
,则面试成绩占比为![]() .
.
由题意,得![]()
![]()
∴笔试成绩占![]() ,面试成绩占
,面试成绩占![]() .
.
(2)2号选手的综合成绩:![]()
3号选手的综合成绩:![]()
∴三位选手按综合成绩排名为:第一名:2号,第二名:1号,第三名:3号.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,点
,点 在边
在边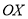 上,
上, .过点
.过点 作
作 于点
于点 ,以
,以 为一边在
为一边在 内作等边
内作等边 ,点
,点 是
是 围成的区域(包括各边)内的一点,过点
围成的区域(包括各边)内的一点,过点 作
作 交
交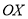 于点
于点 ,作
,作 交
交 于点
于点 .设
.设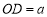 ,
, ,则
,则 最大值是_______.
最大值是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )

A.
 B.
B. 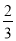 C.
C.  D.
D. 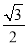
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,已知平面上A、B、C三点,请按照下列语句画出图形:①连接AB;②画射线CA;③画直线BC;

(2)如图2,已知线段AB.
①画图:延长AB到C,使BC=
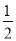 AB;
AB;②若D为AC的中点,且DC=3,求线段AC、BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y1=ax2+bx+c(a≠0)的顶点坐标A(﹣1,3),与x轴的一个交点B(﹣4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a﹣b=0;②abc<0;③抛物线与x轴的另一个交点坐标是(3,0);④方程ax2+bx+c﹣3=0有两个相等的实数根;⑤当﹣4<x<﹣1时,则y2<y1.
其中正确的是( )

A. ①②③ B. ①③⑤ C. ①④⑤ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】现将三张形状、大小完全相同的平行四边形透明纸片分别放在方格纸中,方格纸中的每个小正方形的边长均为1,并且平行四边形 纸片的每个顶点与小正方形的顶点重合(如图①、图②、图③).


图②矩形(正方形)
 ,
,分别在图①、图②、图③中,经过平行四边形纸片的任意一个顶点画一条裁剪线,沿此裁剪线将平行四边形纸片裁成两部分,并把这两部分重新拼成符合下列要求的几何图形.
要求:
(1)在左边的平行四边形纸片中画一条裁剪线,然后在右边相对应的方格纸中,按实际大小画出所拼成的符合要求的几何图形.
(2)裁成的两部分在拼成几何图形时要互不重叠且不留空隙.
(3)所画出的几何图形的各顶点必须与小正方形的顶点重合.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为半圆O的直径,以AO为直径作半圆M,C为OB的中点,D在半圆M上,且CD⊥MD,延长AD交半圆O于点E,且AB=4,则圆中阴影部分的面积为_____________.

相关试题

