Question

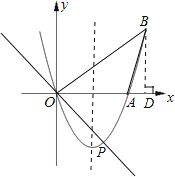
【题目】已知：如图，二次函数y=x2+（2k﹣1）x+k+1的图象与x轴相交于O、A两点．

（1）求这个二次函数的解析式；

（2）在这条抛物线的对称轴右边的图象上有一点B，使锐角△AOB的面积等于3．求点B的坐标．

Answer 1

【答案】（1）y=x2-3x，（2）（4，4）.

【解析】试题分析：（1）将原点坐标代入抛物线中即可求出k的值，也就得出了抛物线的解析式．

（2）根据（1）得出的抛物线的解析式可得出A点的坐标，也就求出了OA的长，根据△OAB的面积可求出B点纵坐标的绝对值，然后将符合题意的B点纵坐标代入抛物线的解析式中即可求出B点的坐标，然后根据B点在抛物线对称轴的右边来判断得出的B点是否符合要求即可．

试题解析：①∵函数的图象与x轴相交于O，

∴0=k+1，

∴k=-1，

∴y=x2-3x，

②假设存在点B，过点B做BD⊥x轴于点D，

∵△AOB的面积等于6，

∴AOBD=6，

当0=x2-3x，

x（x-3）=0，

解得：x=0或3，

∴AO=3，

∴BD=4

即4=x2-3x，

解得：x=4或x=-1（舍去）．

又∵顶点坐标为：（1.5，-2.25）．

∵2.25＜4，

∴x轴下方不存在B点，

∴点B的坐标为：（4，4）.