Question

【题目】（14分）定义：底与腰的比是的等腰三角形叫做黄金等腰三角形．

如图，已知△ABC中，AB=BC，∠C=36°，BA1平分∠ABC交AC于A1．

（1）=AA1A C；

（2）探究：△ABC是否为黄金等腰三角形？请说明理由；（提示：此处不妨设AC=1）

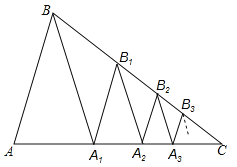
（3）应用：已知AC=a，作A1B1∥AB交BC于B1，B1A2平分∠A1B1C交AC于A2，作A2B2∥AB交B2，B2A3平分∠A2B2C交AC于A3，作A3B3∥AB交BC于B3，…，依此规律操作下去，用含a，n的代数式表示An﹣1An．（n为大于1的整数，直接回答，不必说明理由）

Answer 1

【答案】（1）证明见试题解析；（2）△ABC是黄金等腰三角形；（3）．

【解析】

试题分析：（1）由角平分线的性质和相似三角形的判定与性质，得到△ABC∽△AA1B，从而有，求出即可；

（2）设AC=1，则AB2=1﹣AB，求出AB的值，进而得出=，即可得出结论；

（3）利用（2）中所求进而得出AA1，A1A2的长，进而得出其长度变化规律求出即可．

试题解析：（1）∵AC=BC，∠C=36°，∴∠A=∠ABC=72°，∵BA1平分∠ABC，∴∠ABA1=∠ABC=36°，∴∠C=∠ABA1，又∵∠A=∠A，∴△ABC∽△AA1B，∴，即=AA1A C；

（2）△ABC是黄金等腰三角形，理由：

由（1）知，=AA1A C，设AC=1，∴=AA1，又由（1）可得：AB=A1B，∵∠A1BC=∠C=36°，∴A1B=A1C，∴AB=A1C，∴AA1=AC﹣A1C=AC﹣AB=1﹣AB，∴=1﹣AB，设AB=x，即，∴，解得：，（不合题意舍去），∴AB=，又∵AC=1，∴=，∴△ABC是黄金等腰三角形；

（3）由（2）得；当AC=a，则AA1=AC﹣A1C=AC﹣AB=a﹣AB==，

同理可得：A1A2=A1C﹣A1B1=AC﹣AA1﹣A1B1

===；

故An﹣1An=．