【题目】如果∠A是锐角,则下列结论正确个数为( )个.
①![]() =sinA-1;②sinA+cosA>1;③tanA>sinA;④cosA=sin(90°﹣∠A)
=sinA-1;②sinA+cosA>1;③tanA>sinA;④cosA=sin(90°﹣∠A)
A.1
B.2
C.3
D.4
参考答案:
【答案】C
【解析】解: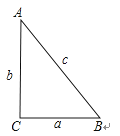
∵在Rt△ACB中,∠C=90°,AC=b,BC=a,AB=c,如图,
sinA=![]() , cosA=
, cosA=![]() , tanA=
, tanA=![]() ,
,
∴![]() =1﹣sinA,sinA+cosA=
=1﹣sinA,sinA+cosA=![]() +
+![]() =
=![]() >1,tanA>sinA,
>1,tanA>sinA,
∵cosA=![]() , sin(90°﹣∠A)=sinB=
, sin(90°﹣∠A)=sinB=![]() ,
,
∴cosA=sin(90°﹣∠A),
即正确的有②③④,共3个,
故选C.
【考点精析】根据题目的已知条件,利用同角三角函数的关系(倒数、平方和商)的相关知识可以得到问题的答案,需要掌握各锐角三角函数之间的关系:平方关系(sin2A+cos2A=1);倒数关系(tanAtan(90°—A)=1);弦切关系(tanA=sinA/cosA ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人相约元旦登山,甲、乙两人距地面的高度y(m)与登山时间x(min)之间的函数图像如图所示,根据图像所提供的信息解答下列问题:
(1)t= min.
(2)若乙提速后,乙登山的上升速度是甲登山的上升速度3倍,
①则甲登山的的上升速度是 m/min;
②请求出甲登山过程中,距地面的高度y(m)与登山时间x(min)之间的函数关系式.
③当甲、乙两人距地面高度差为70m时,求x的值(直接写出满足条件的x值).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆C,点B是该半圆周上一动点,连接OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴、直线OB于点E、F,点E为垂足,连接CF.
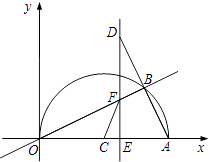
(1)当∠AOB=30°时,求弧AB的长度;
(2)当DE=8时,求线段EF的长;
(3)在点B运动过程中,是否存在以点E、C、F为顶点的三角形与△AOB相似?若存在,请求出此时点E的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
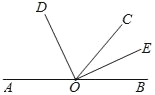
查看答案和解析>>【题目】如图,点 A,O,B 在同一条直线上,OD,OE 分别平分∠AOC 和∠BOC.
(1)求∠DOE 的度数;
(2)如果∠COD=65°,求∠AOE 的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的情况(记向东为正)记录如下(x>5且x<14,单位:m):
行驶次数
第一次
第二次
第三次
第四次
行驶情况
x
﹣
 x
xx﹣3
2(5﹣x)
行驶方向(填“东”或“西”)
(1)请将表格补充完整;
(2)求经过连续4次行驶后,这辆出租车所在的位置;
(3)若出租车行驶的总路程为41m,求第一次行驶的路程x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
A.如图,在△ABC中,∠C=90°.若BD∥AE,∠DBC=20°,则∠CAE的度数是 ;
B.用科学计算器计算: sin58°≈(精确到0.01).
sin58°≈(精确到0.01).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将两条宽度都为3的纸条重叠在一起,使∠ABC=60°,则四边形ABCD的面积为 .

相关试题

