【题目】如图,将两条宽度都为3的纸条重叠在一起,使∠ABC=60°,则四边形ABCD的面积为 .

参考答案:
【答案】6![]() .
.
【解析】
试题分析:先根据两组对边分别平行证明四边形ABCD是平行四边形,再根据两张纸条的宽度相等,利用面积求出AB=BC,然后根据邻边相等的平行四边形是菱形;根据宽度是3cm与∠ABC=60°求出菱形的边长,然后利用菱形的面积=底×高计算即可.
解:∵纸条的对边平行,即AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∵两张纸条的宽度都是3,
∴S四边形ABCD=AB×3=BC×3,
∴AB=BC,
∴平行四边形ABCD是菱形,即四边形ABCD是菱形.
如图,过A作AE⊥BC,垂足为E,
∵∠ABC=60°,
∴∠BAE=90°-60°=30°,
∴AB=2BE,
在△ABE中,AB2=BE2+AE2,
即AB2=![]() AB2+32,
AB2+32,
解得AB=2![]() ,
,
∴S四边形ABCD=BCAE=2![]() ×3=6
×3=6![]() .
.
故答案是:6![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx﹣1(a≠0)的图象经过点(1,1),则代数式3﹣a﹣b的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,点A所表示的实数为3,点B所表示的实数为a,⊙A的半径为2,则下列说法中不正确的是( )
A. 当a﹤5时,点B在⊙A内 B. 当1﹤a﹤5时,点B在⊙A内
C. 当a﹤-1时,点B在⊙A外 D. 当a﹥5时,点B在⊙A外
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用等式的性质解方程:3x+6=31﹣2x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】半径为2cm的与⊙O边长为2cm的正方形ABCD在水平直线l的同侧,⊙O与l相切于点F,DC在l上.
(1)过点B作的一条切线BE,E为切点.
①填空:如图1,当点A在⊙O上时,∠EBA的度数是 ;
②如图2,当E,A,D三点在同一直线上时,求线段OA的长;
(1)以正方形ABCD的边AD与OF重合的位置为初始位置,向左移动正方形(图3),至边BC.与OF重合时结束移动,M,N分别是边BC,AD与⊙O的公共点,求扇形MON的面积的范围.
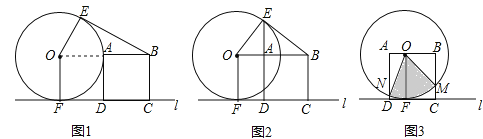
-
科目: 来源: 题型:
查看答案和解析>>【题目】杨辉是我国南宋时期杰出的数学家和教育家,下图是杨辉在公元1261年著作《详解九章算法》里面的一张图,即“杨辉三角”,该图中有很多规律,请仔细观察,解答下列问题:
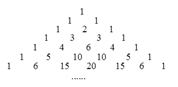
(1)图中给出了七行数字,根据构成规律,第8行中从左边数第3个数是_____;
(2)利用不完全归纳法探索出第n行中的所有数字之和为_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:直线AD,BC被直线CD所截,AC为 ∠BAD的角平分线,∠1+∠BCD=180°.
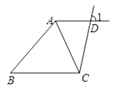
求证:∠BCA=∠BAC.
相关试题

