【题目】如图,在四边形ABCD中,∠BAC=∠ACD=90°,∠B=∠D.若AB=3cm,BC=5cm,点P从B点出发,以1cm/s的速度沿BC→CD→DA运动至A点停止,则从运动开始经过多少时间,△ABP为等腰三角形?


备用图1


备用图2 备用图3
参考答案:
【答案】当点P运动3、2.5、![]() 、10秒时,△APE是等腰三角形
、10秒时,△APE是等腰三角形
【解析】
利用AAS先证明△ABC≌△CDA,可得AD=BC,AB=CD;利用勾股定理先求得AC的长,再根据点P在BC上,点P在CD上,点P在AD上三种情况,结合等腰三角形的判定和勾股定理进行计算即可.
设点P运动的时间为t ,
在△ABC和△CDB中,
∠BAC=∠ACD,∠B=∠D,AC=CA,
∴△ABC≌△CDB(AAS),
∴AD=BC,AB=CD,
在Rt△ABC中,∠BAC=90°,AC=![]() =
=![]() =4.
=4.
设经过ts时,△ABP为等腰三角形.
当P在BC上时,
①BA=BP=3,即t=3时,△ABP为等腰三角形;
②BP=AP=![]() BC=
BC=![]() ,即t=
,即t=![]() 时,△ABP为等腰三角形;
时,△ABP为等腰三角形;
③AB=AP时,如图:

过A作AE⊥BC,垂足为E,AE=![]() ,
,
在Rt△ABE中,BE=![]() =
=![]() =
=![]() .
.
∴BP=2BE=![]() ,
,
即t=![]() 时,△ABP为等腰三角形;
时,△ABP为等腰三角形;
当P在CD上不能得出等腰三角形;
当P在AD上时,只能AB=AP=3,
∴BC+CD+DP=10,即t=10时,△ABP为等腰三角形.
答:从运动开始经过2.5s或3s或![]() s或10s时,△ABP为等腰三角形.
s或10s时,△ABP为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的两个圆盘中,指针落在每一个数上的机会均等,那么两个指针同时落在偶数上的概率是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q.
(1)求证:△ADC≌△BEA;
(2)若PQ=4,PE=1,求AD的长.
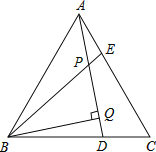
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC,DE∥BC,那么在下列三角形中,与△EBD相似的三角形是( )

A.△ABC
B.△ADE
C.△DAB
D.△BDC -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程.
(1)(x﹣1)2=4;
(2)x2+3x﹣4=0;
(3)4x(2x+1)=3(2x+1);
(4)2x2+5x﹣3=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个布口袋里装有红色、黑色、蓝色和白色的小球各1个,如果闭上眼睛随机地从布袋中取出一个球,记下颜色,放回布袋搅匀,再闭上眼睛随机的再从布袋中取出一个球.求:
(1)连续两次恰好都取出红色球的概率;
(2)连续两次恰好取出一红、一黑的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)观察推理:如图1,△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A、B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D、E.求证:△AEC≌△CDB;
(2)类比探究:如图2,Rt△ABC中,∠ACB=90°,AC=6,将斜边AB绕点A逆时针旋转90°至AB′,连接B′C,求△AB′C的面积.
(3)拓展提升:如图3,等边△EBC中,EC=BC=4cm,点O在BC上,且OC=3cm,动点P从点E沿射线EC以2cm/s速度运动,连结OP,将线段OP绕点O逆时针旋转120°得到线段OF.要使点F恰好落在射线EB上,求点P运动的时间ts.

相关试题

