Question

【题目】（1）观察推理：如图1，△ABC中，∠ACB=90°，AC=BC，直线l过点C，点A、B在直线l同侧，BD⊥l，AE⊥l，垂足分别为D、E．求证：△AEC≌△CDB；

（2）类比探究：如图2，Rt△ABC中，∠ACB=90°，AC=6，将斜边AB绕点A逆时针旋转90°至AB′，连接B′C，求△AB′C的面积．

（3）拓展提升：如图3，等边△EBC中，EC=BC=4cm，点O在BC上，且OC=3cm，动点P从点E沿射线EC以2cm/s速度运动，连结OP，将线段OP绕点O逆时针旋转120°得到线段OF．要使点F恰好落在射线EB上，求点P运动的时间ts．

Answer 1

【答案】（1）详见解析；（2）18；（3）2.5秒．

【解析】

（1）利用同角的余角相等判断出∠CAE=∠BCD，即可得出结论；

（2）先作出高，进而判断出△ABC≌△B'AG，求出B'G，最后用三角形的面积公式即可得出结论；

（3）利用等式的性质得出，∠CPO=∠BOF，进而判断出△BOF≌△PCO，即可求出CP=1，即可得出结论．

（1）∵BD⊥l，AE⊥l，

∴∠AEC=∠CDB=90°，

∴∠CAE+∠ACE=90°，

∵∠ACB=90°，

∴∠ACE+∠BCD=90°，

∴∠CAE=∠BCD，

在△ACE和△CBD中，，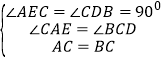

∴△ACE≌△CBD；

（2）如图2，过点B'作B'G⊥AC于G，

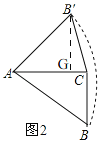
∴∠B'AG+∠AB'G=90°，

∵∠BAB'=90°，

∴∠BAC+∠B'AG=90°，

∴∠AB'G=∠BAC，由旋转知，AB=AB'，

在△ABC和△B'AG中，，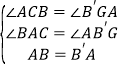

∴△ABC≌△B'AG，

∴B'G=AC=6，

∴S△ACB'=AC×B'G=18；

（3）如图3，

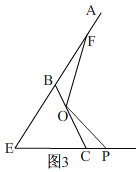
由旋转知，OP=OF，

∵△BCE是等边三角形，

∴∠CBE=∠BCE=60°，

∴∠OCP=∠FBO=120°，∠CPO+∠COP=60°，

∵∠POF=120°，

∴∠COP+∠BOF=60°，

∴∠CPO=∠BOF，

在△BOF和△PCO中，，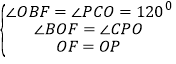

∴△BOF≌△PCO，

∴CP=OB，

∵EC=BC=4cm，OC=3cm，

∴OB=BC﹣OC=1，

∴CP=1，

∴EP=CE+CP=5，

∴点P运动的时间t=5÷2=2.5秒．