【题目】如图,![]() 内接于
内接于![]() ,
,![]() 是直径,
是直径,![]() 的切线
的切线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
![]() 判断
判断![]() 与
与![]() 的位置关系并说明理由;
的位置关系并说明理由;
![]() 若
若![]() 的半径为
的半径为![]() ,
,![]() ,求
,求![]() 的长.
的长.

参考答案:
【答案】![]()
![]() .
.
【解析】
(1)AF为为圆O的切线,理由为:连接OC,由PC为圆O的切线,利用切线的性质得到CP垂直于OC,由OF与BC平行,利用两直线平行内错角相等,同位角相等,分别得到两对角相等,根据OB=OC,利用等边对等角得到一对角相等,等量代换得到一对角相等,再由OC=OA,OF为公共边,利用SAS得出三角形AOF与三角形COF全等,由全等三角形的对应角相等及垂直定义得到AF垂直于OA,即可得证;
(2)由AF垂直于OA,在直角三角形AOF中,由OA与AF的长,利用勾股定理求出OF的长,而OA=OC,OF为角平分线,利用三线合一得到E为AC中点,OE垂直于AC,利用面积法求出AE的长,即可确定出AC的长.
![]() 为圆
为圆![]() 的切线,
的切线,
理由为:
连接![]() ,
,
∵![]() 为圆
为圆![]() 切线,
切线,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵在![]() 和
和![]() 中,
中,
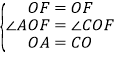 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() 为圆
为圆![]() 的半径,
的半径,
则![]() 为圆
为圆![]() 的切线;
的切线;
![]() 设
设![]() ,由
,由![]() 知
知![]() ,
,![]() ,
,
∴![]() ,
,
且![]() 的半径为
的半径为![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,则
,则![]() ,
,
∴在![]() 中,
中,
![]() ,
,
解得:![]() (舍去)或
(舍去)或![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形纸片
 中,
中,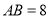 ,将纸片折叠,使顶点
,将纸片折叠,使顶点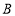 落在边
落在边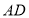 上的
上的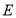 点处,折痕的一端
点处,折痕的一端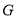 点在边
点在边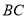 上.
上.(1)如图1,当折痕的另一端
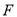 在
在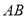 边上且
边上且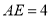 时,求
时,求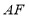 的长
的长(2)如图2,当折痕的另一端
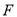 在
在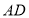 边上且
边上且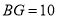 时,
时,①求证:
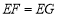 .②求
.②求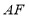 的长.
的长.(3)如图3,当折痕的另一端
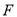 在
在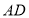 边上,
边上,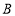 点的对应点
点的对应点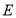 在长方形内部,
在长方形内部,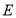 到
到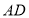 的距离为2
的距离为2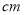 ,且
,且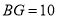 时,求
时,求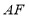 的长.
的长.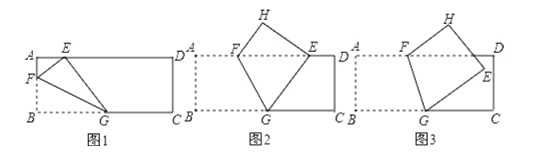
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列条件中,不能证明△ABC ≌ △DCB是( )

A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】北京时间2015年7月31日,国际奥委会主席巴赫宣布:中国北京获得2022年第24届冬季奥林匹克运动会举办权.北京也创造历史,成为第一个既举办过夏奥会又举办冬奥会的城市,张家口也成为本届冬奥会的协办城市.近期,新建北京至张家口铁路可行性研究报告已经获得国家发改委批复,同意新建北京至张家口铁路,铁路全长约180千米.按照设计,京张高铁列车的平均行驶速度是普通快车的1.5倍,用时比普通快车用时少了20分钟,求高铁列车的平均行驶速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的材料,解决问题.
例题:若m2 +2mn+2n2-6n+9=0,求m和n的值.
解:∵ m2+2mn+2n2- 6n+9=0,
∴m2 +2mn+n2+n2-6n+9=0,
∴(m+n)2 +(n-3)2=0,
∴m+n=0, n-3=0,
∴m=-3, n=3.
问题: (1)若2x2 +4x-2xy+y2 +4=0,求xy的值;
(2)已知a, b, c是△ABC的三边长,且满足a2+b2=10a+8b-41,求c的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,以
,以 为直径,
为直径, 为圆心的半圆交
为圆心的半圆交 于点
于点 ,点
,点 为弧
为弧 的中点,连接
的中点,连接 交
交 于点
于点 ,
, 为
为 的角平分线,且
的角平分线,且 ,垂足为点
,垂足为点 .
. 判断直线
判断直线 与
与 的位置关系,并说明理由;
的位置关系,并说明理由;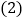 若
若 ,
,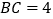 ,求
,求 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一块含45°的直角三角板ABC, AB=AC, ∠BAC=90°, 点D为射线CB上一点,且不与点C,点B重合,连接AD.过点A作线段AD的垂线l,在直线l上,截取AE=AD(点E与点C在直线AD的同侧),连接CE.
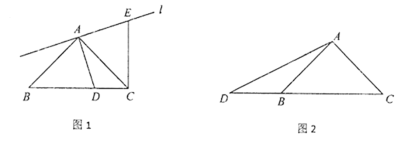
(1)当点D在线段CB上时,如图1,线段CE与BD的数量关系为____________,位置关系为___________;
(2)当点D在线段CB的延长线上时,如图2,
①请将图形补充完整;
②(1)中的结论是否仍成立?如果成立,请证明;如果不成立,请说明理由.
相关试题

