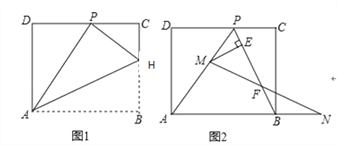
【题目】如图,将矩形ABCD沿AH折叠,使得顶点B落在CD边上的P点处.折痕与边BC交于点 H,
已知AD=8,HC:HB=3:5.
(1)求证:△HCP∽△PDA;
(2) 探究AB与HB之间的数量关系,并证明你的结论;
(3)连结BP,动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;说明理由;若不变,求出线段EF的长度.
参考答案:
【答案】(1)证明见解析;(2)AB=2BH.,理由见解析;(3) EF的长度不变.
【解析】试题分析:(1)根据两角对应相等的两三角形相似可求证;
(2)根据(1)的结论,由相似三角形的性质可求出二者之间的关系;
(3)作MQ∥AB交PB于Q,可得∠MQP=∠ABP, 然后由折叠的性质可知,∠APB=∠ABP,即∠MQP=∠APB,根据等角对等边可得MP=MQ,又BN=PM,根据等量代换可得MQ=BN,然后由平行线分线段成比例可求EF=![]() PB,最后根据勾股定理求解.
PB,最后根据勾股定理求解.
试题解析:(1)由折叠的性质可知,
∠APH=∠B=90°, ∴∠APD+∠HPC=90°,
又∠PHC+∠HPC=90°, ∴∠APD=∠PHC,
又∠D=∠C=90°,∴△HCP∽△PDA;
(2)AB=2BH.
∵HC:HB=3:5,设HC=3x,则HB=5x,
在矩形ABCD中,BC=AD=8 ,∴HC=3,则HB=5
由折叠的性质可知HP=HB=5,AP=AB,
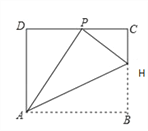
在Rt△HCP,易得PC=4,
∵△HCP∽△PDA
∴![]() ,∴
,∴![]()
∴AB=AP=10=2BH,即AB=2BH.
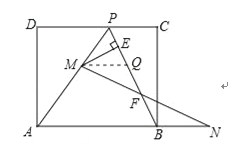
(3)EF的长度不变.
作MQ∥AB交PB于Q, ∴∠MQP=∠ABP,
由折叠的性质可知,∠APB=∠ABP,
∴∠MQP=∠APB,
∴MP=MQ,又BN=PM,∴MQ=BN,
∵MQ∥AB,∴![]() ,
,
∴QF=FB,
∵MP=MQ,ME⊥BP, ∴PE=QE,∴EF=![]() PB,
PB,
由(2)得,PC=4,BC=8,
∴PB=![]() =
=![]() ,
,
∴EF=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的是( )
A. -1的立方根是-1 B. -1的平方是1
C. -1的平方根是-1 D. 1的平方根是±1
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a:b=3:2,且3a-2b=4,则a+b=____.
-
科目: 来源: 题型:
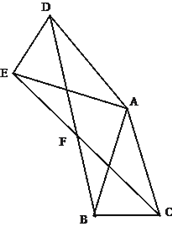
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F,BD交AE于M.
(1)求证:△AEC≌△ADB;
(2)若BC=2,∠BAC=30°,当四边形ADFC是菱形时,求BF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,∠BAD的平分线交BC边于点M,而MD平分∠AMC,若∠MDC=45°,则∠BAD= , ∠ABC=
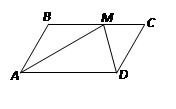
-
科目: 来源: 题型:
查看答案和解析>>【题目】某淘宝店专销某种品牌的运动服,每套进价70元,售价120元/套.为了促销,淘宝店决定凡是一次购买数量不超过10套的,按原价每套120元购买;10套以上的,每多买1套,每套降价1元,每多买2套,每套降价2元…^(例如,某人一次性购买15套运动服,多出5套,按每套降价5元购买,共需(15×115)元;但是最低价90元/套.
(1)求顾客一次至少买多少套,才能以最低价购买?,
(2)写出当一次购买
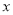 (
(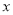 >10)件时,利润
>10)件时,利润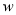 (元)与购买量
(元)与购买量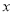 (件)之间的函数关系式;
(件)之间的函数关系式;(3)有一天,一位顾客买了35套运动服,另一位顾客买了40套运动服,淘宝店发现卖了40套反而比卖35套赚的钱少!为了使每次卖的数量多赚的钱也多,在其它促销条件不变的情况下,最低价为90元/套至少要提高到多少?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】设点A(﹣1,y1)、B(1,y2)、C(2,y3)是抛物线y=﹣2(x﹣1)2+m上的三点,则y1、y2,y3的大小关系的是_____(用“<”连接).
相关试题

