【题目】自主学习,请阅读下列解题过程.
解一元二次不等式:![]() >0.
>0.
解:设![]() =0,解得:
=0,解得:![]() =0,
=0,![]() =5,则抛物线y=
=5,则抛物线y=![]() 与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=
与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=![]() 的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即
的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即![]() >0,所以,一元二次不等式
>0,所以,一元二次不等式![]() >0的解集为:x<0或x>5.
>0的解集为:x<0或x>5.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
(1)上述解题过程中,渗透了下列数学思想中的 和 .(只填序号)
①转化思想 ②分类讨论思想 ③数形结合思想
(2)一元二次不等式![]() <0的解集为 .
<0的解集为 .
(3)用类似的方法解一元二次不等式:![]() >0.
>0.
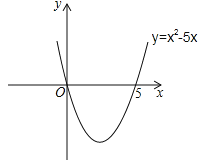
参考答案:
【答案】(1)①,③;(2)0<x<5;(3)x<﹣1或x>3.
【解析】
试题分析:(1)根据题意容易得出结论;
(2)由图象可知:当0<x<5时函数图象位于x轴下方,此时y<0,即![]() <0,即可得出结果;
<0,即可得出结果;
(3)设![]() =0,解方程得出抛物线y=
=0,解方程得出抛物线y=![]() 与x轴的交点坐标,画出二次函数y=
与x轴的交点坐标,画出二次函数y=![]() 的大致图象,由图象可知:当x<﹣1,或x>5时函数图象位于x轴上方,此时y>0,即
的大致图象,由图象可知:当x<﹣1,或x>5时函数图象位于x轴上方,此时y>0,即![]() >0,即可得出结果.
>0,即可得出结果.
试题解析:(1)上述解题过程中,渗透了下列数学思想中的①和③;
故答案为:①③;
(2)由图象可知:当0<x<5时函数图象位于x轴下方,此时y<0,即![]() <0,∴一元二次不等式
<0,∴一元二次不等式![]() <0的解集为:0<x<5;
<0的解集为:0<x<5;
故答案为:0<x<5.
(3)设![]() =0,解得:
=0,解得:![]() =3,
=3,![]() =﹣1,∴抛物线y=
=﹣1,∴抛物线y=![]() 与x轴的交点坐标为(3,0)和(﹣1,0).
与x轴的交点坐标为(3,0)和(﹣1,0).
画出二次函数y=![]() 的大致图象(如图所示),由图象可知:当x<﹣1,或x>3时函数图象位于x轴上方,此时y>0,即
的大致图象(如图所示),由图象可知:当x<﹣1,或x>3时函数图象位于x轴上方,此时y>0,即![]() >0,∴一元二次不等式
>0,∴一元二次不等式![]() >0的解集为:x<﹣1或x>3.
>0的解集为:x<﹣1或x>3.
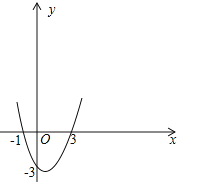
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个三角形的各边长扩大为原来的5倍,则此三角形的周长扩大为原来的 倍.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市广播电视局欲招聘播音员一名,对A,B两名候选人进行了两项素质测试,两人的两项测试成绩如表所示.
测试项目
测试成绩
A
B
面试
90
95
综合知识测试
85
80
根据实际需要,广播电视局将面试、综合知识测试的得分按3:2的比例计算两人的总成绩,那么(填A或B)将被录用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个三角形的两边长分别为5和8,则第三边长可能是( )
A.13B.10C.3D.2
-
科目: 来源: 题型:
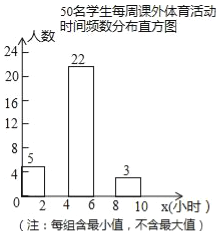
查看答案和解析>>【题目】为增强学生体质,各学校普遍开展了阳光体育活动,某校为了解全校1000名学生每周课外体育活动时间的情况,随机调查了其中的50名学生,对这50名学生每周课外体育活动时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周课外体育活动时间在6≤x<8小时的学生人数占24%.根据以上信息及统计图解答下列问题:
(1)本次调查属于 调查,样本容量是 ;
(2)请补全频数分布直方图中空缺的部分;
(3)求这50名学生每周课外体育活动时间的平均数;
(4)估计全校学生每周课外体育活动时间不少于6小时的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
(1)求证:△ACD∽△BFD;
(2)当tan∠ABD=1,AC=3时,求BF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】读一读:式子“1+2+3+4+5+…+100”表示1开始的100个连续自然数的和.由于上述式子比较长,书写也不方便,为了简便起见,我们可以将“1+2+3+4+5+…+100”表示为
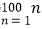 ,这里“
,这里“ ”是求和符号.例如:1+3+5+7+9+…+99,即从1开始的100以内的连续奇数的和,可表示为
”是求和符号.例如:1+3+5+7+9+…+99,即从1开始的100以内的连续奇数的和,可表示为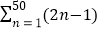 ;又如13+23+33+43+53+63+73+83+93+103可表示为
;又如13+23+33+43+53+63+73+83+93+103可表示为 .
.通过对上以材料的阅读,请解答下列问题:
(1)2+4+6+8+10+…+100(即从2开始的100以内的连续偶数的和)用求和符号可表示为__________;
(2)计算
 =________________.(填写最后的计算结果)
=________________.(填写最后的计算结果)
相关试题

