【题目】如图,已知△ABC为等边三角形,AB=2,点D为边AB上一点,过点D作DE∥AC,交BC于E点;过E点作EF⊥DE,交AB的延长线于F点.设AD=x,△DEF的面积为y,则能大致反映y与x函数关系的图象是( )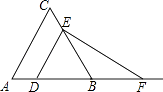
A.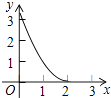
B.
C.
D.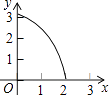
参考答案:
【答案】A
【解析】解:∵△ABC是等边三角形,
∴∠B=60°,
∵DE∥AC,
∴∠EDF=∠B=60°,
∵EF⊥DE,
∴∠DEF=90°,
∴∠F=90°﹣∠EDC=30°;
∵∠ACB=60°,∠EDC=60°,
∴△EDB是等边三角形.
∴ED=DB=2﹣x,
∵∠DEF=90°,∠F=30°,
∴EF= ![]() ED=
ED= ![]() (2﹣x).
(2﹣x).
∴y= ![]() EDEF=
EDEF= ![]() (2﹣x)
(2﹣x) ![]() (2﹣x),
(2﹣x),
即y= ![]() (x﹣2)2 , (x<2),
(x﹣2)2 , (x<2),
故选A.
根据平行线的性质可得∠EDF=∠B=60°,根据三角形内角和定理即可求得∠F=30°,然后证得△EDB是等边三角形,从而求得ED=DB=2﹣x,再根据直角三角形的性质求得EF,最后根据三角形的面积公式求得y与x函数关系式,根据函数关系式即可判定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,直线a∥b,点
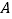 、
、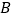 分别在
分别在 、
、 上,且
上,且 ,
,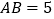 .点
.点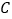 、
、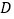 从
从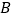 点同时出发,分别以1个单位/秒,2个单位/秒的速度,在直线b上沿相反方向运动.设运动
点同时出发,分别以1个单位/秒,2个单位/秒的速度,在直线b上沿相反方向运动.设运动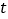 秒后,得到△ACD.(友情提醒:本题的结果可用根号表示)
秒后,得到△ACD.(友情提醒:本题的结果可用根号表示)(1)当
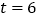 秒时,点
秒时,点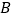 到直线
到直线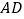 的距离为 ;
的距离为 ;(2)若△ACD是直角三角形,t的值为 ;
(3)若△ACD是等腰三角形,求t的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,△ABC的高CD与角平分线AE相交点F,过点C作CH⊥AE于G,交AB于H.下列说法:①∠BCH=∠CAE;②DF=EF;③CE=BH;④S△ABE=2S△ACE;⑤CF=
 DF.正确的是_____.
DF.正确的是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一根绳子对折成一条线段AB,在线段AB取一点P,使AP=
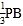 ,从P处把绳子剪断,若剪断后的三段绳子中最长的一段为30cm,则绳子的原长为______cm.
,从P处把绳子剪断,若剪断后的三段绳子中最长的一段为30cm,则绳子的原长为______cm. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
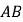 与
与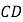 相交于点
相交于点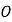 ,
,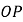 是
是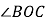 的平分线,
的平分线,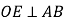 ,
,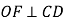 .
.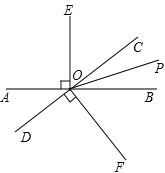
(1)若
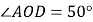 ,请求出
,请求出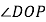 的度数;
的度数;(2)
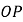 平分
平分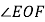 吗?为什么?
吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,矩形OABC的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E,那么点D的坐标为()

A.(﹣ ,
,  )
)
B.(﹣ ,
,  )
)
C.(﹣ ,
,  )
)
D.(﹣ ,
,  )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为半圆O的直径,AD、BC分别切⊙O于A,B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2 , ④OD:OC=DE:OE,⑤OD2=DECD,正确的有( )
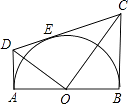
A.2个
B.3个
C.4个
D.5个
相关试题

