【题目】如图,在△ABC中,∠ACB=90°,AC=BC,△ABC的高CD与角平分线AE相交点F,过点C作CH⊥AE于G,交AB于H.下列说法:①∠BCH=∠CAE;②DF=EF;③CE=BH;④S△ABE=2S△ACE;⑤CF=![]() DF.正确的是_____.
DF.正确的是_____.

参考答案:
【答案】①③⑤
【解析】
①根据同角的余角相等可得结论正确;
②如图1,作辅助线,构建三角形的内心为F,根据角平分线的性质得:DF=FM,由垂线段最短可知:EF>FM,则EF>DF;
③如图1,证明△ACF≌△CBH,可得CF=BH=CE,可作判断;
④如图2,连接EH,FH,先证明四边形CFHE是菱形,得CD∥EH,则EH⊥AB,所以△EHB是等腰直角三角形,则BE=![]() EH=
EH=![]() CE,根据三角形面积公式可得S△ABE=
CE,根据三角形面积公式可得S△ABE=![]() S△ACE;
S△ACE;
⑤如图2,易得△ADF≌△CDH,由△FDH是等腰直角三角形,则FH=![]() DF,所以CF=FH=
DF,所以CF=FH=![]() DF.
DF.
①∵∠ACB=90°,
∴∠CAE+∠AEC=90°,
∵CH⊥AE,
∴∠CGE=90°,
∴∠BCH+∠AEC=90°,
∴∠BCH=∠CAE;
故①正确;
②如图1,连接FB,过F作FM⊥BC于M,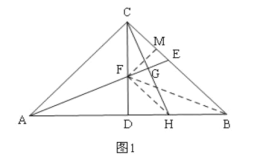
∵AC=BC,CD⊥AB,
∴CD平分∠ACB,
∵AE平分∠CAB,
∴BF平分∠ABC,
∵FD⊥AB,
∴DF=FM,
Rt△FME中,∠AEC=45°+22.5°=67.5°,
∴EF>FM,
即EF>DF,
故②不正确;
③如图1,∵∠DCH=∠BCH,AE⊥CG,
∴∠CFG=∠CEF,
∴CF=CE,
在△ACF和△CBH中,
∵∠HCB=∠FAC,BC=AC,∠B=∠ACF=45°,
∴△ACF≌△CBH,
∴CF=BH=CE,
故③正确;
④如图2,连接EH,FH,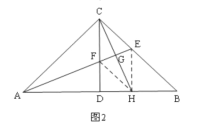
∵∠AHC=∠B+∠BCH=45°+22.5°=67.5°,
∠ACH=90°∠BCH=67.5°,
∴∠AHC=∠ACH,
∴AC=AH,
∵AE⊥CH,
∴CG=GH,
∵CF=CE,
∴GF=GE,
∴四边形CFHE是菱形,
∴CD∥EH,
∵CD⊥AB,
∴EH⊥AB,
∴△EHB是等腰直角三角形,
∴BE=![]() EH=
EH=![]() CE,
CE,
∵S△ABE=![]() BEAC,
BEAC,
S△ACE=![]() CEAC,
CEAC,
∴S△ABE=![]() S△ACE,
S△ACE,
故④不正确;
⑤如图2,易得△ADF≌△CDH,
∴DF=DH,
∴∠FHD=45°,
∴△FDH是等腰直角三角形,
∴FH=![]() DF,
DF,
∵∠AHC=67.5°,
∴∠FHC=∠FCH=22.5°,
∴CF=FH=![]() DF,
DF,
故⑤正确;
综上所述,正确的是:①③⑤
故答案为:①③⑤.
-
科目: 来源: 题型:
查看答案和解析>>【题目】山东全省2016年国庆假期旅游人数增长12.5%,其中尤其是乡村旅游最为火爆.泰山脚下的某旅游村,为接待游客住宿需要,开设了有100张床位的旅馆,当每张床位每天收费100元时,床位可全部租出,若每张床位每天收费提高20元,则相应的减少了10张床位租出,如果每张床位每天以20元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
A.140元
B.150元
C.160元
D.180元 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一根起点为1的数轴,现有同学将它弯折,弯折后虚线上第一行的数是1,第二行的数是13,第三行的数是43,…,依此规律,第五行的数是( )
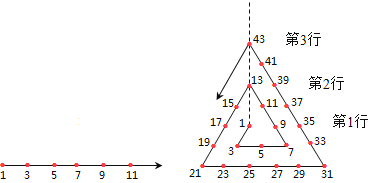
A. 183 B. 157 C. 133 D. 91
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,直线a∥b,点
 、
、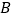 分别在
分别在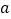 、
、 上,且
上,且 ,
,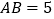 .点
.点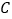 、
、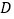 从
从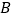 点同时出发,分别以1个单位/秒,2个单位/秒的速度,在直线b上沿相反方向运动.设运动
点同时出发,分别以1个单位/秒,2个单位/秒的速度,在直线b上沿相反方向运动.设运动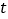 秒后,得到△ACD.(友情提醒:本题的结果可用根号表示)
秒后,得到△ACD.(友情提醒:本题的结果可用根号表示)(1)当
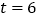 秒时,点
秒时,点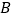 到直线
到直线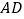 的距离为 ;
的距离为 ;(2)若△ACD是直角三角形,t的值为 ;
(3)若△ACD是等腰三角形,求t的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把一根绳子对折成一条线段AB,在线段AB取一点P,使AP=
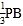 ,从P处把绳子剪断,若剪断后的三段绳子中最长的一段为30cm,则绳子的原长为______cm.
,从P处把绳子剪断,若剪断后的三段绳子中最长的一段为30cm,则绳子的原长为______cm. -
科目: 来源: 题型:
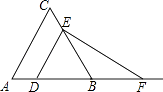
查看答案和解析>>【题目】如图,已知△ABC为等边三角形,AB=2,点D为边AB上一点,过点D作DE∥AC,交BC于E点;过E点作EF⊥DE,交AB的延长线于F点.设AD=x,△DEF的面积为y,则能大致反映y与x函数关系的图象是( )
A.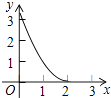
B.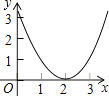
C.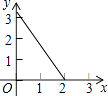
D.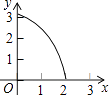
-
科目: 来源: 题型:
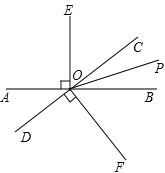
查看答案和解析>>【题目】如图,直线
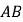 与
与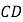 相交于点
相交于点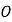 ,
,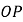 是
是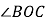 的平分线,
的平分线,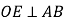 ,
,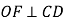 .
.
(1)若
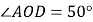 ,请求出
,请求出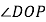 的度数;
的度数;(2)
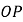 平分
平分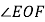 吗?为什么?
吗?为什么?
相关试题

