【题目】如图,菱形OABC的一边OA在x轴上,将菱形OABC绕原点O顺时针旋转75°至OA′B′C′的位置,若OB= ![]() ,∠C=120°,则点B′的坐标为( )
,∠C=120°,则点B′的坐标为( ) 
A.(3, ![]() )
)
B.(3, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.( ![]() ,
, ![]() )
)
参考答案:
【答案】D
【解析】解:过点B作BE⊥OA于E,过点B′作B′F⊥OA于F, ∴∠BE0=∠B′FO=90°,
∵四边形OABC是菱形,
∴OA∥BC,∠AOB= ![]() ∠AOC,
∠AOC,
∴∠AOC+∠C=180°,
∵∠C=120°,
∴∠AOC=60°,
∴∠AOB=30°,
∵菱形OABC绕原点O顺时针旋转75°至OA′B′C′的位置,
∴∠BOB′=75°,OB′=OB=2 ![]() ,
,
∴∠B′OF=45°,
在Rt△B′OF中,
OF=OB′cos45°=2 ![]() ×
× ![]() =
= ![]() ,
,
∴B′F= ![]() ,
,
∴点B′的坐标为:( ![]() ,﹣
,﹣ ![]() ).
).
故选D.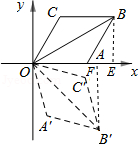
首先根据菱形的性质,即可求得∠AOB的度数,又由将菱形OABC绕原点O顺时针旋转75°至OA′B′C′的位置,可求得∠B′OA的度数,然后在Rt△B′OF中,利用三角函数即可求得OF与B′F的长,则可得点B′的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙的成绩分析如表所示,丁的成绩如图所示.
甲
乙
丙
平均数
7.9
7.9
8.0
方差
3.29
0.49
1.8
根据以上图表信息,参赛选手应选( )

A.甲
B.乙
C.丙
D.丁 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AB于点E.

(1)求证:∠E=∠C;
(2)若⊙O的半径为3,AD=2,试求AE的长;
(3)求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,F是
 上一点,且
上一点,且  =
= 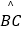 ,连接CF并延长交AD的延长线于点E,连接AC,若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
,连接CF并延长交AD的延长线于点E,连接AC,若∠ABC=105°,∠BAC=25°,则∠E的度数为( ) 
A.45°
B.50°
C.55°
D.60° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△AOB的值为( )

A.1:3
B.1:5
C.1:6
D.1:11 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=
 x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为
x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为  ,则a、b的值分别为( )
,则a、b的值分别为( ) 
A. ,
, 
B. ,﹣
,﹣ 
C. ,﹣
,﹣ 
D.﹣ ,
, 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,正方形A1B1C1D1、D1 E1E2B2、A2B2 C2D2、D2E3E4B3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为l,∠B1C1O=60°,B1C1∥B2C2∥B3C3…,则正方形A2017B2017C2017 D2017的边长是( )

A.( )2016
)2016
B.( )2017
)2017
C.( )2016
)2016
D.( )2017
)2017
相关试题

