【题目】(1)己知:如图,△ABC,∠C=90°,现将斜边AB绕A点顺时针旋转90°到AD,过D点作DE⊥CA,交CA的延长线于点E.求证:△ABC ≌ △DAE
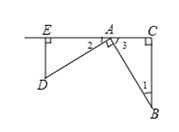
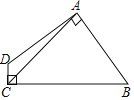
(2)如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为 。
参考答案:
【答案】(1)见解析(2)![]()
【解析】
(1)根据垂直的性质得到∠1=∠2,,利用AAS即可证明△ABC ≌ △DAE;
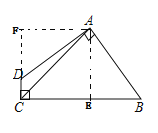
(2)过A点作BC的垂直交于E,过点A作CD的延长线于点F,根据(1)可知△AFD≌△AEB,故四边形ABCD的面积等于正方形AECF的面积,再根据AC为对角线即可求解.
(1)∵将斜边AB绕A点顺时针旋转90°到AD,
∴∠BAD=90°,AD=AB
∠2+∠3=90°,
∵∠C=90°
∴∠1+∠3=90°,
∴∠1=∠2,
又DE⊥CA
∴△ABC ≌ △DAE(AAS)
(2)过A点作BC的垂直交于E,过点A作CD的延长线于点F,
∵∠DAB=∠DCB=90°=∠F,
四边形AECF为矩形,
∵AB=AD,∠DAB=90°,
根据(1)可知△AFD≌△AEB,
∴AF=AE,
∴矩形AECF为正方形,
由△AFD≌△AEB
∴四边形ABCD的面积等于正方形AECF的面积,
∵AC是正方形AECF的对角线,
∴S正方形AECF=![]() ×AC2=
×AC2=![]()
故四边形ABCD的面积等于![]() .
.
-
科目: 来源: 题型:
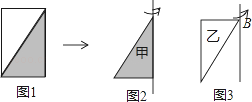
查看答案和解析>>【题目】如图1,把一张长10厘米、宽6厘米的长方形纸板分成两个相同的直角三角形.
(1)甲三角形(如图2)旋转一周,可以形成一个怎样的几何体?它的体积是多少立方米?
(2)乙三角形(如图3)旋转一周,可以形成一个怎样的几何体?它的体积是多少立方米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】学完《全等三角形》知识后知道:满足“SSA”的两个三角形不一定全等,如图①,∠A与AB分别是△ABC与△ABD公共角与公共边,且AC=AD,但△ABC与△ABD不全等,但在特殊条件下“SSA”也可以确定两个三角形全等.如图②,∠MAB为锐角,AB=5,点B到射线AM的距离为3,点C在射线AM上,BC=x,当x的取值范围是__________时,△ABC的形状、大小是唯一确定。
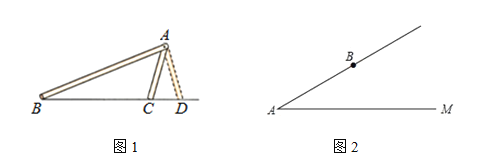
-
科目: 来源: 题型:
查看答案和解析>>【题目】将矩形纸片
 按如图的方式折叠,得到菱形
按如图的方式折叠,得到菱形 ,若
,若 ,则
,则 的长为( )
的长为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径为6cm,B为⊙O外一点,OB交⊙O于点A,AB=OA,动点P从点A出发,以π cm/s的速度在⊙O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为______时,BP与⊙O相切.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,B、C分别是∠PAQ的两边AP,AQ上的点,直线l垂直平分BC。

(1)尺规作图:在直线1上求作一点O,使得点O到AP、AQ距离相等(不写作法,保留作图痕迹);
(2)过O点作OE⊥AP,OF⊥AQ,垂足分别为E、F。求证BE=CF
-
科目: 来源: 题型:
查看答案和解析>>【题目】邮递员骑摩托车从邮局出发,先向东骑行2km到达A村,继续向东骑行3km到达B村,然后向西骑行9km到C村,最后回到邮局.
(1)以邮局为原点,以向东方向为正方向,用1个单位长度表示1km,请你在数轴上表示出A、B、C三个村庄的位置;

(2)C村离A村有多远?
(3)若摩托车每1km耗油0.03升,这趟路共耗油多少升?
相关试题

