【题目】已知:如图,B、C分别是∠PAQ的两边AP,AQ上的点,直线l垂直平分BC。

(1)尺规作图:在直线1上求作一点O,使得点O到AP、AQ距离相等(不写作法,保留作图痕迹);
(2)过O点作OE⊥AP,OF⊥AQ,垂足分别为E、F。求证BE=CF
参考答案:
【答案】(1)图见解析(2)见解析
【解析】
(1)根据题意作∠QAP的角平分线与l的交点即为O点;
(2)连接BO、CO,再根据角平分线上的点到角的两边距离相等可得OE=OF,根据线段垂直平分线上的点到两端点的距离相等可得BO=CO,然后利用“HL”证明Rt△BOE和Rt△COF全等,根据全等三角形对应边相等证明即可.
(1)如图所示,AO是∠QAP的角平分线,AO与l的交点即为所求O点;
(2)证明:连接BO、CO,
∵AO是∠BAC的平分线,
∴OE=OF,
∵l是BC边的垂直平分线,
∴BO=CO,
在Rt△BOE和Rt△COF中,
![]()
∴Rt△BOE≌Rt△COF(HL),
∴BE=CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将矩形纸片
 按如图的方式折叠,得到菱形
按如图的方式折叠,得到菱形 ,若
,若 ,则
,则 的长为( )
的长为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
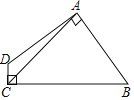
查看答案和解析>>【题目】(1)己知:如图,△ABC,∠C=90°,现将斜边AB绕A点顺时针旋转90°到AD,过D点作DE⊥CA,交CA的延长线于点E.求证:△ABC ≌ △DAE
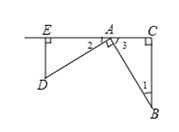
(2)如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径为6cm,B为⊙O外一点,OB交⊙O于点A,AB=OA,动点P从点A出发,以π cm/s的速度在⊙O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为______时,BP与⊙O相切.

-
科目: 来源: 题型:
查看答案和解析>>【题目】邮递员骑摩托车从邮局出发,先向东骑行2km到达A村,继续向东骑行3km到达B村,然后向西骑行9km到C村,最后回到邮局.
(1)以邮局为原点,以向东方向为正方向,用1个单位长度表示1km,请你在数轴上表示出A、B、C三个村庄的位置;

(2)C村离A村有多远?
(3)若摩托车每1km耗油0.03升,这趟路共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某地,人们发现在一定温度下某种蟋蟀叫的次数与温度之间有如下的近似关系:用蟋蟀1min叫的次数除以7,然后再加上3,就近似地得到该地当时的温度(℃).
(1)用代数式表示该地当时的温度;
(2)当蟋蟀1min叫的次数分别是84,105和126时,该地当时的温度约是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】世界杯比赛中,根据场上攻守形势,守门员会在门前来回跑动,如果以球门线为基准,向前跑记作正数,返回则记作负数,一段时间内,某守门员的跑动情况记录如下(单位:m):+10,﹣2,+5,﹣6,+12,﹣9,+4,﹣14.(假定开始计时时,守门员正好在球门线上)
(1)守门员最后是否回到球门线上?
(2)守门员离开球门线的最远距离达多少米?
(3)如果守门员离开球门线的距离超过10米(不包括10米),则对方球员挑射极可能造成破门.请问在这一时间段内,对方球员有几次挑射破门的机会?

相关试题

