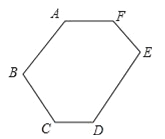
【题目】如图,六边形ABCDEF中,AF∥CD,AB∥DE,∠A=140°,∠B=100°,∠E=90°,求:∠C、∠D、∠F的度数.
参考答案:
【答案】∠C=120°,∠CDE=140°,∠F=130°.
【解析】试题分析:连接AD,由AF∥CD得出∠FAD=∠ADC,由AB∥DE得出∠BAD=∠ADE,故可得出∠CDE=∠BAF,∠FAD+∠ADE=∠ADC+∠BAD=∠BAF,再由四边形内角和定理即可得出∠F与∠C的度数.
试题解析:
连接AD,
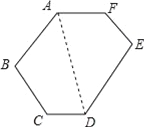
∵AF∥CD,
∴∠FAD=∠ADC.
∵AB∥DE,
∴∠BAD=∠ADE,
∴∠CDE=∠BAF=140°,
∴∠FAD+∠ADE=∠ADC+∠BAD=∠BAF=140°.
∵∠E=90°,
∴∠F=360°﹣140°﹣90°=130°.
∵∠B=100°,
∴∠C=360°﹣100°﹣140°=120°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农民在自己家承包的甲、乙两片荒山上各栽了200棵苹果树,成活率均为96%,现已挂果.他随意从甲山采摘了4棵树上的苹果,称得质量(单位:千克)分别为36,40,48,36;从乙山采摘了4棵树上的苹果,称得质量(单位:千克)分别为50,36,40,34,将这两组数据组成一个样本,回答下列问题:
(1)样本容量是多少?
(2)样本平均数是多少?并估算出甲、乙两山苹果的总产量;
(3)甲、乙两山哪个山上的苹果长势较整齐?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在正方形ABCD中,AB=6,P为边CD上一点,过P点作PE⊥BD于点E,连接BP.

(1) 如图1,求
 的值;
的值;(2)O为BP的中点,连接CO并延长交BD于点F.
① 如图2,连接OE,求证:OE⊥OC;
② 如图3,若
 ,求DP的长.
,求DP的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】嘉兴市2010~2014年社会消费品零售总额及增速统计图如下:
请根据图中信息,解答下列问题:
(1)求嘉兴市2010~2014年社会消费品零售总额增速这组数据的中位数.
(2)求嘉兴市近三年(2012~2014年)的社会消费品零售总额这组数据的平均数.
(3)用适当的方法预测嘉兴市2015年社会消费品零售总额(只要求列出算式,不必计算出结果).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,补充条件后仍不一定能保证△ABC≌△A′B′C′,则补充的这个条件是( )
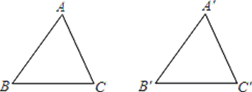
A. BC=B′C′ B. ∠A=∠A′ C. AC=A′C′ D. ∠C=∠C′
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
 与
与 轴交于点A,点B(1,0),与
轴交于点A,点B(1,0),与 轴交于点C(0,﹣3),点M是其顶点.
轴交于点C(0,﹣3),点M是其顶点.(1)求抛物线解析式;
(2)第一象限抛物线上有一点D,满足∠DAB=45°,求点D的坐标;
(3)直线
 (﹣3<
(﹣3< <﹣1)与x轴相交于点H.与线段AC,AM和抛物线分别相交于点E,F,P.证明线段HE,EF,FP总能组成等腰三角形.
<﹣1)与x轴相交于点H.与线段AC,AM和抛物线分别相交于点E,F,P.证明线段HE,EF,FP总能组成等腰三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】某特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
相关试题

