【题目】已知一次函数y=2x-4的图象与x轴、y轴分别相交于点A、B,点P在该函数的图象上,P到x轴、y轴的距离分别为d1,d2。
(1)求点A,B的坐标;
(2)当P为线段AB的中点时,求d1+d2的值;
(3)直接写出d1+d2的范围,并求当d1+d2=3时点P的坐标;
(4)若在线段AB上存在无数个点P,使d1+ad2=4(a为常数),求a的值。
参考答案:
【答案】(1)A(2,0)B(0,-4);(2)d1+d2=3;(3)当d1+d2=3时点的坐标为点p1(1,2)、p2(![]() ,
,![]() );(4)在线段上存在无数个p点, a=2.
);(4)在线段上存在无数个p点, a=2.
【解析】
(1)对于一次函数解析式,分别令y=0求出x的值,令x=0,求出y的值,即可求出A与B的坐标,
(2)求出P点坐标,即可求出d1+d2的值;.
(3)根据题意确定出d1+d2的范围,设P(m,2m-4),表示出d1+d2,分类讨论m的范围,根据d1+d2=3求出m的值,即可确定出P的坐标;.
(4)设P(m,2m-4),表示出d1与d2,由P在线段上求出m的范围,利用绝对值的代数意义表示出d1与d2,代入d1+ad2=4,根据存在无数个点P求出a的值即可.
(1)如图所示,
令y=0时,x=2, x=0时,y =-4,
∴A(2,0)B(0,-4)
(2)当为线段的中点时,P(![]() ,
,![]() ) 即P(1,-2)
) 即P(1,-2)
∴d1+d2=3
(3)d1+d2≥2
∵P点在一次函数y=2x-4的图象上,故设点P(m,2m-4),
∴d1+d2=︱xp︱+︱yp︱=︱m︱+︱2m-4︱.
由题当d1+d2=3时,根据2m-4=2(m-2)可分析,
当0≤m≤2时,d1+d2=m+4-2m=3,此时解得,m=1∴得点p1(1,2).
当m>2时,同理, d1+d2=m+2m-4=3,解得m=![]() ,所以得点p2(
,所以得点p2(![]() ,
,![]() ).
).
当m<0时,d1+d2=-m+4-2m=3,解得m=![]() ,即不符合m<0,故此时不存在点p.
,即不符合m<0,故此时不存在点p.
综上所述,当d1+d2=3时点的坐标为点p1(1,2)、p2(![]() ,
,![]() ).
).
(4)设点P(m,2m-4),
∴d1=︱2m-4︱,d2=︱m︱,
∵P在线段AB上,且点A(2,0),B(0,-4),
∴0≤m≤2.即d1=4-2m,d2=m.
∵使d1+ad2=4(
∴代入数值得4-2m+am=4,即(a-2)m=0,
根据题意在线段上存在无数个p点,所以a=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某花店准备购进甲、乙两种花卉,若购进甲种花卉20盆,乙种花卉50盆,需要720元;若购进甲种花卉40盆,乙种花卉30盆,需要880元.
(1)求购进甲、乙两种花卉,每盆各需多少元?
(2)该花店销售甲种花卉每盆可获利6元,销售乙种花卉每盆可获利1元,现该花店准备拿出800元全部用来购进这两种花卉,设购进甲种花卉x盆,全部销售后获得的利润为W元,求W与x之间的函数关系式;
(3)在(2)的条件下,考虑到顾客需求,要求购进乙种花卉的数量不少于甲种花卉数量的6倍,且不超过甲种花卉数量的8倍,那么该花店共有几种购进方案?在所有的购进方案中,哪种方案获利最大?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上A点表示数﹣2,B点表示数6,若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,则经过 秒,甲、乙两小球到原点的距离相等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】提出问题:
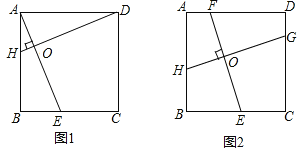
(1)如图1,在正方形ABCD中,点E,H分别在BC,AB上,若AE⊥DH于点O,求证:AE=DH;
类比探究:
(2)如图2,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,若EF⊥HG于点O,探究线段EF与HG的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,二次函数y=﹣
 x2+bx+c的图线与坐标轴分别交于点A、B、C,其中点A(0,8),OB=
x2+bx+c的图线与坐标轴分别交于点A、B、C,其中点A(0,8),OB= OA.
OA.(1)求二次函数的表达式;
(2)若OD=OB,点F为该二次函数在第二象限内图象上的动点,E为DF的中点,当△CEF的面积最大时,求出点E的坐标;
(3)将三角形CEF绕E旋转180°,C点落在M处,若M恰好在该抛物线上,求出此时△CEF的面积.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AC=3,AB=5,点O在BC边的中线AD上,⊙O与BC相切于点E,且∠OBA=∠OBC.
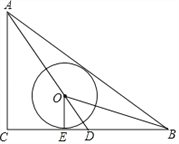
(1)求证:AB为⊙O的切线;
(2)求⊙O的半径;
(3)求tan∠BAD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的大括号内:
﹣5,|-
 |,﹣12,0,﹣3.14,+1.99,﹣(﹣6),
|,﹣12,0,﹣3.14,+1.99,﹣(﹣6),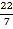
(1)正数集合:{ …}
(2)负数集合:{ …}
(3)整数集合:{ …}
(4)分数集合:{ …}.
相关试题

