【题目】如图,△ABC中,∠C=90°,AC=3,AB=5,点O在BC边的中线AD上,⊙O与BC相切于点E,且∠OBA=∠OBC.
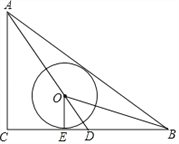
(1)求证:AB为⊙O的切线;
(2)求⊙O的半径;
(3)求tan∠BAD.
参考答案:
【答案】(1)详见解析;(2)⊙O的半径为![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)作OF垂直AB于点F,然后根据角平分线的性质定理即可证得OE=OF,从而证得结论;
(2)根据勾股定理求得![]() ,进而求得
,进而求得![]() 设
设![]() 的半径为r,然后根据
的半径为r,然后根据![]() 得到
得到![]()
解关于r的方程即可求得半径;
(3)证得Rt△ODE∽Rt△ADC,根据相似三角形的性质求得![]() ,
,
即可求得![]() ,
, ![]() ,解直角三角形即可求得
,解直角三角形即可求得![]() .
.
试题解析:
(1)证明:如图,作OF垂直AB于点F,
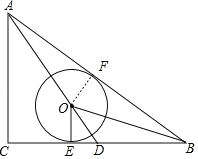
∵⊙O与BC相切于点E,
∴OE⊥BC,
又∠OBA=∠OBC,
∴OE=OF,
∴AB为![]() 的切线 ;
的切线 ;
(2)∵∠C=90,AC=3,AB=5,
![]() 又D为BC的中点,
又D为BC的中点,
∴CD=DB=2,
![]()
设⊙O的半径为r,即
![]()
∴6+2r+5r=12
![]()
∴⊙O的半径为![]()
(3) ![]() ,OE⊥BC,
,OE⊥BC,
∴OE∥AC,
∴Rt△ODE∽Rt△ADC,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】提出问题:
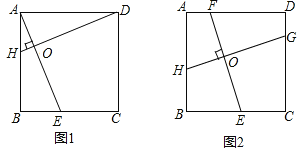
(1)如图1,在正方形ABCD中,点E,H分别在BC,AB上,若AE⊥DH于点O,求证:AE=DH;
类比探究:
(2)如图2,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,若EF⊥HG于点O,探究线段EF与HG的数量关系,并说明理由.
-
科目: 来源: 题型:
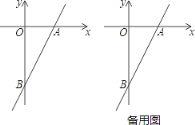
查看答案和解析>>【题目】已知一次函数y=2x-4的图象与x轴、y轴分别相交于点A、B,点P在该函数的图象上,P到x轴、y轴的距离分别为d1,d2。
(1)求点A,B的坐标;
(2)当P为线段AB的中点时,求d1+d2的值;
(3)直接写出d1+d2的范围,并求当d1+d2=3时点P的坐标;
(4)若在线段AB上存在无数个点P,使d1+ad2=4(a为常数),求a的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,二次函数y=﹣
 x2+bx+c的图线与坐标轴分别交于点A、B、C,其中点A(0,8),OB=
x2+bx+c的图线与坐标轴分别交于点A、B、C,其中点A(0,8),OB= OA.
OA.(1)求二次函数的表达式;
(2)若OD=OB,点F为该二次函数在第二象限内图象上的动点,E为DF的中点,当△CEF的面积最大时,求出点E的坐标;
(3)将三角形CEF绕E旋转180°,C点落在M处,若M恰好在该抛物线上,求出此时△CEF的面积.


-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的大括号内:
﹣5,|-
 |,﹣12,0,﹣3.14,+1.99,﹣(﹣6),
|,﹣12,0,﹣3.14,+1.99,﹣(﹣6),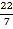
(1)正数集合:{ …}
(2)负数集合:{ …}
(3)整数集合:{ …}
(4)分数集合:{ …}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)|﹣3|﹣5×(﹣
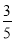 )+(﹣4)
)+(﹣4)(2)(﹣2)2﹣4÷(﹣
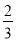 )+(﹣1)2016
)+(﹣1)2016(3)
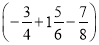 ×(﹣24)
×(﹣24)(4)﹣12014﹣(1﹣0.5)÷
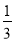 ×[(﹣2)3﹣4]
×[(﹣2)3﹣4] -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)4(2x﹣1)﹣3(5x+1)=14
(2)5﹣
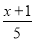 =x
=x(3)
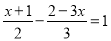
(4)
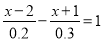
相关试题

