【题目】如图,已知抛物线经过坐标原点O和x轴上另一点E,顶点M的坐标为(2,4);矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3.
(1)求该抛物线所对应的函数关系式;
(2)将矩形ABCD以每秒1个单位长度的速度从如图所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀速移动,设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图2所示).
①当t=![]() 时,判断点P是否在直线ME上,并说明理由;
时,判断点P是否在直线ME上,并说明理由;
②设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.

参考答案:
【答案】(1)![]() ;(2)①不在;②最大值为
;(2)①不在;②最大值为![]() .
.
【解析】
试题分析:(1)已知顶点坐标,又抛物线经过原点,用待定系数可求出抛物线解析式;
(2)①根据抛物线的对称性求出E点坐标,再求出直线ME的解析式,把t知代入验证点P是否在直线ME上;
②最后一问设出P,N坐标,根据几何关系求出PN,然后分两种情况讨论:(1)PN=0;(2)PN≠0;把求多边形面积S转化为求函数最值问题.
试题解析:(1)因所求抛物线的顶点M的坐标为(2,4),故可设其关系式为![]() ,又∵抛物线经过O(0,0),∴得
,又∵抛物线经过O(0,0),∴得![]() ,解得a=﹣1,∴所求函数关系式为
,解得a=﹣1,∴所求函数关系式为![]() ,即
,即![]() .
.
(2)①点P不在直线ME上.根据抛物线的对称性可知E点的坐标为(4,0),又M的坐标为(2,4),设直线ME的关系式为y=kx+b.于是得:![]() ,解得:
,解得:![]() ,所以直线ME的关系式为y=﹣2x+8.
,所以直线ME的关系式为y=﹣2x+8.
由已知条件易得,当t=![]() 时,OA=AP=
时,OA=AP=![]() ,∴P(
,∴P(![]() ,
,![]() ).
).
∵P点的坐标不满足直线ME的关系式y=﹣2x+8,∴当t=![]() 时,点P不在直线ME上.
时,点P不在直线ME上.
②S存在最大值.理由如下:
∵点A在x轴的非负半轴上,且N在抛物线上,∴OA=AP=t,∴点P,N的坐标分别为(t,t)、(t,![]() ),∴AN=
),∴AN=![]() (0≤t≤3),∴AN﹣AP=(
(0≤t≤3),∴AN﹣AP=(![]() )﹣t=
)﹣t=![]() =t(3﹣t)≥0,∴PN=
=t(3﹣t)≥0,∴PN=![]() .(ⅰ)当PN=0,即t=0或t=3时,以点P,N,C,D为顶点的多边形是三角形,此三角形的高为AD,∴S=
.(ⅰ)当PN=0,即t=0或t=3时,以点P,N,C,D为顶点的多边形是三角形,此三角形的高为AD,∴S=![]() DCAD=
DCAD=![]() ×3×2=3.
×3×2=3.
(ⅱ)当PN≠0时,以点P,N,C,D为顶点的多边形是四边形.
∵PN∥CD,AD⊥CD,∴S=![]() (CD+PN)AD=
(CD+PN)AD=![]() =
=![]() =
=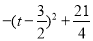 ,其中(0<t<3),由a=﹣1,0<
,其中(0<t<3),由a=﹣1,0<![]() <3,此时S最大=
<3,此时S最大=![]() .
.
综上所述,当t=![]() 时,以点P,N,C,D为顶点的多边形面积有最大值,这个最大值为
时,以点P,N,C,D为顶点的多边形面积有最大值,这个最大值为![]() .
.
说明:(ⅱ)中的关系式,当t=0和t=3时也适合.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当我们利用2种不同的方法计算同一图形的面积时,可以得到一个等式.例如,由图1,可得等式:(a+2b)(a+b)=a2+3ab+2b2 .
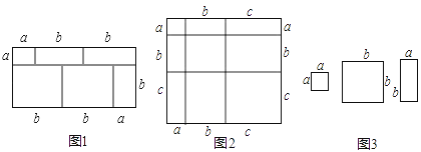
(1)由图2,可得等式:
(2)利用(1)中所得到的结论,解决下面的问题:已知 a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)利用图3中的纸片(足够多),画出一种拼图,使该拼图可用来验证等式:2a2+5ab+2b2=(2a+b)(a+2b);
(4)小明用2 张边长为a 的正方形,3 张边长为b的正方形,5 张边长分别为a、b 的长方形纸片重新拼出一个长方形,那么该长方形较长的一条边长为 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=12cm,BC=24cm,如果将该矩形沿对角线BD折叠,那么图中阴影部分的面积( )cm2 .

A.72
B.90
C.108
D.144 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列变形正确的是( )
A.4x﹣5=3x+2变形得4x﹣3x=﹣2+5
B.﹣3x=2变形得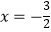
C.3(x﹣1)=2(x+3)变形得3x﹣1=2x+6
D. 变形得4x﹣6=3x+18
变形得4x﹣6=3x+18 -
科目: 来源: 题型:
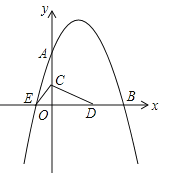
查看答案和解析>>【题目】如图,已知抛物线
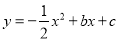 与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.(1)直接写出抛物线的解析式: ;
(2)求△CED的面积S与D点运动时间t的函数解析式;当t为何值时,△CED的面积最大?最大面积是多少?
(3)当△CED的面积最大时,在抛物线上是否存在点P(点E除外),使△PCD的面积等于△CED的最大面积?若存在,求出P点的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=30°,点P在∠AOB内部且OP=4,P1与P关于OB对称,P2与P关于OA对称,则P1P2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算及解方程:
(1)化简:(5a2﹣ab)﹣2(3a2﹣ ab)
ab)
(2)解方程: ﹣
﹣  =1
=1
(3)先化简,再求值:3x2y﹣[2xy﹣2(xy﹣ x2y)+xy],其中x=3,y=﹣
x2y)+xy],其中x=3,y=﹣  .
.
相关试题

