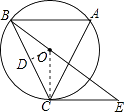
【题目】如图,⊙O是△ABC的外接圆,∠A=60°,过点C作⊙O的切线,交射线BO于点E. 
(1)求∠BCE的度数;
(2)若⊙O半径为3,求BE长.
参考答案:
【答案】
(1)解:连接OC,∵∠A=60°,∴∠BOC=120°,
又∵OB=OC,∴∠OCB=∠OBC=30°,
∵EC切⊙O于E,∴∠OCE=90°,
∴∠ECB=120°
(2)解:过点O作OD⊥BC于点D,
∵∠A=60°,
∴∠BOC=120°,
又∵∠CBE=∠BOC,
∴△BOC∽△BCE,
∴ ![]() =
= ![]()
∴BC2=BOBE;
∵BO=3,∠OBD=30°,
∴BD=BOcos30°= ![]() ,
,
∴BC=3 ![]() ,
,
∴(3 ![]() )2=3BE,
)2=3BE,
∴BE=9.
【解析】(1)利用切线的性质结合等腰三角形的性质得出∠OCE=90°,∠OCB=∠OBC=30°,进而求出∠BCE的度数;(2)利用相似三角形的判定与性质得出△BOC∽△BCE,进而得出 ![]() =
= ![]() ,进而得出答案.
,进而得出答案.
【考点精析】通过灵活运用切线的性质定理,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(背景知识)数轴上有两点 A、B 对应的数为 a、b,AB表示这两个点间的距离,这两个点的中点所对应的数为
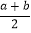 .
.已知数轴上有三点 A、B、C,对应的数分别为 a、b、c,a、b、c 满足以下两个条件:①
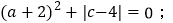 ② a-b+c=0.
② a-b+c=0.(1)求出 a、b、c 的值;
(2)若数轴上有一点 P,PA=3PB,求出满足条件的P点所对应的数;
(3)点A以每秒钟2个单位长度的速度向左运动,点B以每秒钟4个单位长度的速度向右运动,点C以每秒钟6个单位长度的速度向右运动.它们同时出发,M为AB 的中点,N为BC的中点,Q为AC的中点,O为原点,试求
 的值.
的值. -
科目: 来源: 题型:
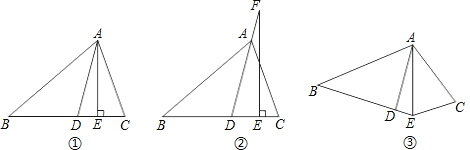
查看答案和解析>>【题目】如图①,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°.
(1)求∠DAE的度数;
(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数;
(3)如图③,若把“AE⊥BC”变成“AE平分∠BEC”,其它条件不变,∠DAE的大小是否变化,并请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将两张半径均为10的半圆形的纸片完全重合叠放一起,上面这张纸片绕着直径的一端B顺时针旋转30°后得到如图所示的图形,
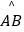 与直径AB交于点C,连接点C与圆心O′.
与直径AB交于点C,连接点C与圆心O′. 
(1)求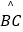 的长;
的长;
(2)求图中下面这张半圆形纸片未被上面这张纸片重叠部分的面积S白 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,∠A:∠B:∠C=2:3:4,CD是∠ACB平分线,求∠A和∠CDB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】七年级(1)班有学生60人,其中参加数学小组的学生有36人,参加英语小组的学生比参加数学小组的学生少5人,并且这两个小组都不参加的人数比两个小组都参加的人数的
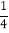 多2人,则同时参加这两个小组的人数是( )
多2人,则同时参加这两个小组的人数是( )A. 16 B. 12 C. 10 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,外角∠EAB,∠ABF的平分线AD、BD相交于点D,求∠D的度数.

相关试题

