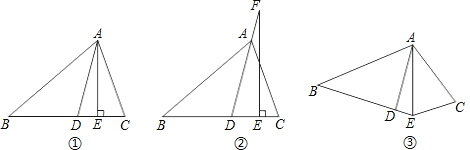
【题目】如图①,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°.
(1)求∠DAE的度数;
(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数;
(3)如图③,若把“AE⊥BC”变成“AE平分∠BEC”,其它条件不变,∠DAE的大小是否变化,并请说明理由.
参考答案:
【答案】(1)∠DAE =15°;(2)∠DFE=15°;(3)∠DAE的度数大小不变.
【解析】
(1)求出∠ADE的度数,利用∠DAE=90°∠ADE即可求出∠DAE的度数;
(2)求出∠ADE的度数,利用∠DFE=90°∠ADE即可求出∠DFE的度数;
(3)利用AE平分∠BEC,AD平分∠BAC,求出∠DFE=15°即是最好的证明.
(1)∵∠B=40°,∠C=70°,
∴∠BAC=70°,
∵AD平分∠BAC,
∴∠BAD=∠CAD=35°,
∴∠ADE=∠B+∠BAD=75°,
∵AE⊥BC,
∴∠AEB=90°,
∴∠DAE=90°-∠ADE=15°.
(2)同(1),可得,∠ADE=75°,
∵FE⊥BC,
∴∠FEB=90°,
∴∠DFE=90°-∠ADE=15°.
(3)结论:∠DAE的度数大小不变.
证明:∵AE平分∠BEC,
∴∠AEB=∠AEC,
∴∠C+∠CAE=∠B+∠BAE,
∵∠CAE=∠CAD-∠DAE,∠BAE=∠BAD+∠DAE,
∴∠C+∠CAD-∠DAE=∠B+∠BAD+∠DAE,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴2∠DAE=∠C-∠B=30°,
∴∠DAE=15°.
-
科目: 来源: 题型:
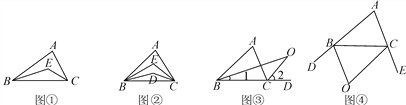
查看答案和解析>>【题目】【问题】如图①,在△ABC中,BE平分∠ABC,CE平分∠ACB,若∠A=80°,则∠BEC=__ __;若∠A=n°,则∠BEC=__ _.
【探究】
(1)如图②,在△ABC中,BD,BE三等分∠ABC,CD,CE三等分∠ACB.若∠A=n°,则∠BEC=____;
(2)如图③,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC和∠A有怎样的关系?请说明理由;
(3)如图④,O是外角∠DBC与外角∠BCE的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠BAC的平分线AD交BC于点D,DE垂直平分AC,垂足为点E,∠BAD=29°,求∠B的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(背景知识)数轴上有两点 A、B 对应的数为 a、b,AB表示这两个点间的距离,这两个点的中点所对应的数为
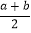 .
.已知数轴上有三点 A、B、C,对应的数分别为 a、b、c,a、b、c 满足以下两个条件:①
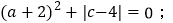 ② a-b+c=0.
② a-b+c=0.(1)求出 a、b、c 的值;
(2)若数轴上有一点 P,PA=3PB,求出满足条件的P点所对应的数;
(3)点A以每秒钟2个单位长度的速度向左运动,点B以每秒钟4个单位长度的速度向右运动,点C以每秒钟6个单位长度的速度向右运动.它们同时出发,M为AB 的中点,N为BC的中点,Q为AC的中点,O为原点,试求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】将两张半径均为10的半圆形的纸片完全重合叠放一起,上面这张纸片绕着直径的一端B顺时针旋转30°后得到如图所示的图形,
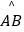 与直径AB交于点C,连接点C与圆心O′.
与直径AB交于点C,连接点C与圆心O′. 
(1)求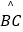 的长;
的长;
(2)求图中下面这张半圆形纸片未被上面这张纸片重叠部分的面积S白 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,∠A=60°,过点C作⊙O的切线,交射线BO于点E.

(1)求∠BCE的度数;
(2)若⊙O半径为3,求BE长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,∠A:∠B:∠C=2:3:4,CD是∠ACB平分线,求∠A和∠CDB的度数.

相关试题

