【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.

参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据相“HL”定理得出△BDE≌△CDF,故可得出DE=DF,所以AD平分∠BAC;
(2)由(1)中△BDE≌△CDE可知BE=CF,AD平分∠BAC,故可得出△AED≌△AFD,所以AE=AF,故AB+AC=AE-BE+AF+CF=AE+AE=2AE.
(1)证明:∵DE⊥AB于E,DF⊥AC于F,
∴∠E=∠DFC=90°,
∴△BDE与△CDE均为直角三角形,
∵![]() ,
,
∴△BDE≌△CDF,
∴DE=DF,即AD平分∠BAC;
(2)AB+AC=2AE.
证明:∵BE=CF,AD平分∠BAC,
∴∠EAD=∠CAD,
∵∠E=∠AFD=90°,
∴∠ADE=∠ADF,
在△AED与△AFD中,
∵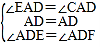 ,
,
∴△AED≌△AFD,
∴AE=AF,
∴AB+AC=AE-BE+AF+CF=AE+AE=2AE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于三个数
 ,用
,用 表示这三个数中最大数,例如:
表示这三个数中最大数,例如: ,
,
解决问题:
(1)填空:
 {
{ ,
, ,
, }= ,如果
}= ,如果 {
{ ,
, ,
, }=
}= ,则
,则 的取值范围为 ;
的取值范围为 ;(2)如果
 {
{ ,
, ,
, }=
}= ,求
,求 的值;
的值;(3)如图,在同一坐标系中画出了三个一次函数的图象:
 ,
, 和
和

请观察这三个函数的图象,
①在图中画出
 {
{ ,
, ,
, }对应的图像(加粗);
}对应的图像(加粗);②
 {
{ ,
, ,
, }的最小值为 .
}的最小值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】基本图形:在Rt△
 中,
中, ,
, 为
为 边上一点(不与点
边上一点(不与点 ,
,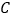 重合),将线段
重合),将线段 绕点
绕点 逆时针旋转
逆时针旋转 得到
得到 .
.探索:(1)连接
 ,如图①,试探索线段
,如图①,试探索线段 之间满足的等量关系,并证明结论;
之间满足的等量关系,并证明结论;(2)连接
 ,如图②,试探索线段
,如图②,试探索线段 之间满足的等量关系,并证明结论;
之间满足的等量关系,并证明结论; 
联想:(3)如图③,在四边形
 中,
中, .若
.若 ,
,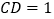 ,则
,则 的长为 .
的长为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:

(1)△AEF≌△CEB;
(2)AF=2CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,数轴被折成
 ,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3。先让圆周上数字2所对应的点与数轴上的数3所对应的点重合,数轴固定,圆紧贴数轴沿着数轴的正方向滚动,那么数轴上的数2009将与圆周上的数字_________重合。
,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3。先让圆周上数字2所对应的点与数轴上的数3所对应的点重合,数轴固定,圆紧贴数轴沿着数轴的正方向滚动,那么数轴上的数2009将与圆周上的数字_________重合。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在△ABC中,D为BC边上的一点,延长AD到点E,连接BE、CE,
∠ABD+
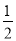 ∠3=90°,∠1=∠2=∠3,下列结论:①△ABD为等腰三角形;②AE=AC;③BE=CE=CD;④CB平分∠ACE.其中正确的结论个数有( )
∠3=90°,∠1=∠2=∠3,下列结论:①△ABD为等腰三角形;②AE=AC;③BE=CE=CD;④CB平分∠ACE.其中正确的结论个数有( )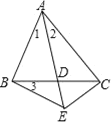
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂家生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD,线段CD分别表示该产品每千克生产成本y1(单位:元),销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
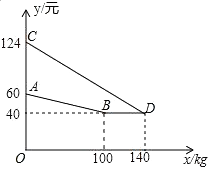
(1)请解释图中点D的实际意义.
(2)求线段CD所表示的y2与x之间的函数表达式.
(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?
相关试题

