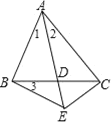
【题目】已知,如图,在△ABC中,D为BC边上的一点,延长AD到点E,连接BE、CE,
∠ABD+![]() ∠3=90°,∠1=∠2=∠3,下列结论:①△ABD为等腰三角形;②AE=AC;③BE=CE=CD;④CB平分∠ACE.其中正确的结论个数有( )
∠3=90°,∠1=∠2=∠3,下列结论:①△ABD为等腰三角形;②AE=AC;③BE=CE=CD;④CB平分∠ACE.其中正确的结论个数有( )
A.1个B.2个C.3个D.4个
参考答案:
【答案】C
【解析】
可根据证△ABF≌△△ADF推出AB=AD,得出△ABD为等腰三角形;可根据同弦所对的圆周角相等点A、B、C、E共圆,可判出BE=CE=CD,根据三角形内角和等于180°,可判出AE=AC;求出∠7=90°﹣![]() ∠2,根据∠1=∠4=∠2推出∠4≠∠7,即可得出BC不是∠ACE的平分线.
∠2,根据∠1=∠4=∠2推出∠4≠∠7,即可得出BC不是∠ACE的平分线.
解:作AF平分∠BAD,

∵∠BAD=∠3,∠ABD+![]() ∠3=90°,
∠3=90°,
∴∠BAF=![]() ∠3=∠DAF,
∠3=∠DAF,
∴∠ABF+∠BAF=90°
∴∠AFB=∠AFD=90°,
在△BAF和△DAF中

∴△ABF≌△ADF(ASA),
∴AB=AD,∴①正确;
∵∠BAD=∠2=∠3,
∴点A、B、E、C在同一个圆上,
∴∠BAE=∠4=∠3,∠ABC=∠6,
∴BE=CE,
∵∠5=∠ADB=∠ABD,∠BAE=∠4,
∴∠5=∠6,
∴CE=CD,
即CD=CE=BE,∴③正确;
∵∠6+∠2+∠ACE=180°,∠6=∠5=∠ADB=∠ABD=90°﹣![]() ∠2.
∠2.
∴∠ACE=180°﹣∠6﹣∠2=90°﹣![]() ∠2,
∠2,
∴∠ACE=∠6,
∴AE=CE,∴②正确
∵∠5=∠2+∠7=90°﹣![]() ∠2,
∠2,
∴∠7=90°﹣![]() ∠2,
∠2,
∵∠BAD=∠4=∠2,
∴∠4≠∠7,∴④错误;
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:

(1)△AEF≌△CEB;
(2)AF=2CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,数轴被折成
 ,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3。先让圆周上数字2所对应的点与数轴上的数3所对应的点重合,数轴固定,圆紧贴数轴沿着数轴的正方向滚动,那么数轴上的数2009将与圆周上的数字_________重合。
,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3。先让圆周上数字2所对应的点与数轴上的数3所对应的点重合,数轴固定,圆紧贴数轴沿着数轴的正方向滚动,那么数轴上的数2009将与圆周上的数字_________重合。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂家生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD,线段CD分别表示该产品每千克生产成本y1(单位:元),销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
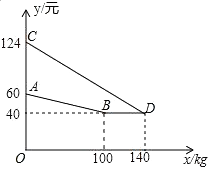
(1)请解释图中点D的实际意义.
(2)求线段CD所表示的y2与x之间的函数表达式.
(3)当该产品产量为多少时,获得的利润最大?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】图象中所反应的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离,根据图象提供的信息,以下四个说法错误的是( )
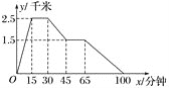
A. 体育场离张强家2.5千米 B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店4千米 D. 张强从早餐店回家的平均速度是
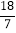 千米/小时
千米/小时 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙A和⊙B的半径分别为5和1,AB=3,点O在直线AB上,⊙O与⊙A、⊙B都内切,那么⊙O半径是 .

相关试题

