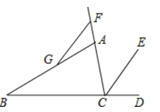
【题目】如图,CE是∠ACD的角平分线,F为CA延长线上一点,G为线段AB上一点,连接FG.
(1)若∠ACD=110°,∠AFG=55°,试说明:FG∥CE
(2)若∠AGF=20°,∠BAC=45°,且FG∥CE,求∠ACE的度数
参考答案:
【答案】(1)证明见解析;(2)∠ACE =25°.
【解析】
(1)根据角平分线的定义求出∠ACE,可知∠ACE=∠AFG,根据内错角相等,两直线平行即可判定FG//CE;
(2)根据三角形外角的性质求出∠AFG,再根据两直线平行,内错角相等即可求出∠ACE.
解:(1)∵CE是∠ACD的角平分线,∠ACD=110°,
∴![]() ,
,
又∵∠AFG=55°,
∴∠ACE=∠AFG,
∴FG∥CE;
(2)∵∠AGF=20°,∠BAC=45°,
∴∠AFG=∠BAC-∠AGF=25°,
∵FG∥CE,
∴∠ACE=∠AFG=25°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图为放置在水平桌面上的台灯的平面示意图,灯臂AO长为40cm,与水平面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°,求该台灯照亮水平面的宽度BC(不考虑其他因素,结果精确到0.1cm.温馨提示:sin75°≈0.97,cos75°≈0.26,
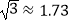 ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员A:月销售件数200件,月总收入3400元;
营业员B:月销售件数300件,月总收入3700元;
假设营业员的月基本工资为x元,销售每件服装奖动y元.
(1)求x和y的值;
(2)商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲服装3件,乙服装2件,丙服袋1件共需390元:如果购买甲服装1件,乙服装2件,丙服装3件共需370元.某顾客想购买甲、乙、丙服装各一件共需多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面说法错误的是( )
A.过一点有且只有一条直线与已知直线垂直.
B.在同一个平面内,任意三条直线相交,交点的个数最多有3个
C.平行于同一直线的两条直线平行.
D.两条平行线被第三条直线所截,一对内错角的平分线互相平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC是ABCD的对角线,∠BAC=∠DAC.

(1)求证:AB=BC;
(2)若AB=2,AC=2
 ,求ABCD的面积.
,求ABCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB∥DC,∠B=90°,F为DC上一点,且FC=AB,E为AD上一点,EC交AF于点G.
(1)求证:四边形ABCF是矩形;
(2)若ED=EC,求证:EA=EG.

-
科目: 来源: 题型:
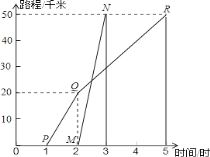
查看答案和解析>>【题目】如图所示,甲、乙两人沿相同的路线由A到B行进,他们行进的路程与出发后的时间(h)之间的函数图象如图所示,根据图象信息,图中的折线PQR和线段MN分别表示甲乙所行驶的路程S和时间t的关系.
根据图象回答下列问题:
(1)A、B两地相距多远?
(2)甲和乙哪一个早到达B城?早多长时间?
(3)甲在QR段的速度是多少?
相关试题

