【题目】有30箱苹果,以每箱20千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质质量的差 (单位:千克) |
|
|
| 1 | 2 |
箱数 | 2 | 6 | 10 | 8 | 4 |
(1)这30箱苹果中,最重的一箱比最轻的一箱重多少千克?
(2)与标准质量比较,这30箱苹果总计超过或不足多少千克?
(3)若苹果每千克售价6元,则出售这30箱苹果可卖多少元?
参考答案:
【答案】(1)3.5;(2)多2千克;(3)5760元.
【解析】
(1)最重的一箱苹果比标准质量重2千克,最轻的一箱苹果比标准质量轻1.5千克,则两箱相差3.5千克;
(2)将这30个数据相加,和为正,表示比标准质量超过,和为负表示比标准质量不足,再求绝对值即可;
(3)先求得总质量,再乘以6元即可.
(1)2(1.5)=3.5(千克).
答:最重的一箱比最轻的一箱多重3.5千克;
(2)(1.5×2)+(1×6)+(0.5×10)+(1×8)+(2×4) =365+8+8=2(千克).
答:30箱苹果的平均质量比标准质量多2千克;
(3)[30×(30+2)]×6=960×6=5760(元).
答:出售这30箱苹果可卖5760元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(-8)+10-2+(-1); (2)12-7×(-4)+8÷(-2);
(3)(
 )÷(-
)÷(- ); (4)-14-(1+0.5)×
); (4)-14-(1+0.5)× ÷(-4)2.
÷(-4)2. -
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入相应的集合内:
4.2 , 50% , 0 , ,
 , 2.122222…, 3.01001…,
, 2.122222…, 3.01001…, ,
,  ,
, 
正数集合:{ };
分数集合:{ };
负有理数集合:{ };
无理数集合:{ }.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, ⊙O 的半径是2,直线l与⊙O 相交于A、B 两点,M、N 是⊙O 上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB 面积的最大值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两班举行电脑汉字输入比赛,各选10名选手参赛,各班参赛学生每分钟输入汉字个数统计如下表:
输入汉字个数(个)
132
133
134
135
136
137
甲班人数人)
1
0
2
4
1
2
乙班人数(人)
0
1
4
1
2
2
请分别判断下列同学是说法是否正确,并说明理由.
(1)两个班级输入汉字个数的平均数相同;
(2)两个班学生输入汉字的中位数相同众数也相同;
(3)甲班学生比乙班学生的成绩稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上点
 表示的数是
表示的数是 点
点 在点
在点 的右侧,且到点
的右侧,且到点 的距离是18;点
的距离是18;点 在点
在点 与点
与点 之间,且到点
之间,且到点 的距离是到点
的距离是到点 距离的2倍.
距离的2倍.(1)点
 表示的数是____________;点
表示的数是____________;点 表示的数是_________;
表示的数是_________;(2)若点P从点
 出发,沿数轴以每秒4个单位长度的速度向右匀速运动;同时,点Q从点B出发,沿数轴以每秒2个单位长度的速度向左匀速运动。设运动时间为
出发,沿数轴以每秒4个单位长度的速度向右匀速运动;同时,点Q从点B出发,沿数轴以每秒2个单位长度的速度向左匀速运动。设运动时间为 秒,在运动过程中,当
秒,在运动过程中,当 为何值时,点P与点Q之间的距离为6?
为何值时,点P与点Q之间的距离为6?(3)在(2)的条件下,若点P与点C之间的距离表示为PC,点Q与点B之间的距离表示为
 在运动过程中,是否存在某一时刻使得
在运动过程中,是否存在某一时刻使得 ?若存在,请求出此时点
?若存在,请求出此时点 表示的数;若不存在,请说明理由.
表示的数;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形
 ,对角线
,对角线 交于点
交于点 ,点
,点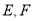 分别是
分别是 的中点,连接
的中点,连接 交
交 于
于 ,连接
,连接

(1)证明:四边形
 是平行四边形
是平行四边形(2)点
 是哪些线段的中点,写出结论,并选择一组给出证明.
是哪些线段的中点,写出结论,并选择一组给出证明.
相关试题

