【题目】已知某市2017年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图所示. 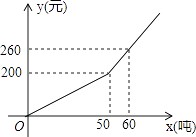
(1)当0≤x≤50时,求y关于x的函数关系式;
(2)当50≤x≤60时,求y关于x的函数关系式;
(3)若某企业3月份用水量为40吨,求该企业3月份应交的水费;
(4)若某企业5月份用水量为620吨,求该企业在5月份的用水量.
参考答案:
【答案】
(1)解:当0≤x≤50时,设y关于x的函数关系式为y=kx
∵y=kx经过(50,200),
∴50k=200,
∴k=4,
y=4x
(2)解:设y关于x的函数关系式y=k′x+b′,
∵直线y=k′x+b′经过点(50,200),(60,260)
∴ ![]() 解得
解得 ![]() ,
,
∴y关于x的函数关系式是y=6x﹣100
(3)解:∵40<50,
∴当x=40时,y=4×40=160元.
∴该企业3月份应交的水费160元
(4)解:由图可知,当y=620时,x>50,
∴6x﹣100=620,
解得x=120.
∴该企业2013年10月份的用水量为120吨.
【解析】(1)当0≤x≤50时,设y关于x的函数关系式为y=kx,利用待定系数法即可 解决问题;(2)设y关于x的函数关系式y=kx+b,代入(50,200)、(60,260)两点求得解析式即可;(3)利用(1)中 关系式即可解决问题;(4)把y=620代入(1)求得答案即可;
-
科目: 来源: 题型:
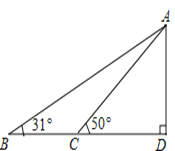
查看答案和解析>>【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m)
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中具有稳定性的是( )
A.菱形B.钝角三角形C.长方形D.正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据:3,1,3,5,3,2 的众数是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)
如图,已知AB∥CD,BE、CF分别平分∠ABC和∠DCB,求证:BE∥CF.

证明:
∵AB∥CD,(已知)
∴∠_____=∠_____.( )
∵ ,(已知)
∴∠EBC=
 ∠ABC.(角的平分线定义)
∠ABC.(角的平分线定义)同理,∠FCB= .
∴∠EBC=∠FCB.(等式性质)
∴BE∥CF.( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】八(1)班组织了一次食品安全知识竞赛,甲、乙两队各5人的成绩如表所示(10分制).
甲
8
10
9
6
9
乙
10
8
9
7
8
(1)甲队成绩的中位数是分;
(2)乙队成绩的众数是分;
(3)分别计算甲队、乙队的方差;并判断哪队的成绩更稳定?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连结BE,CF.
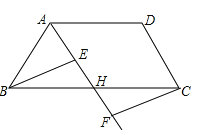
(1)请你添加一个条件,使得△BEH≌△CFH,你添加的条件是 ,并证明.
(2)在问题(1)中,当BH与EH满足什么关系时,四边形BFCE是矩形,请说明理由.
相关试题

