【题目】计算题
(1)(3ab)2(﹣![]() ab3)
ab3)
(2)20182﹣2016×2020(利用乘法公式计算)
(3)﹣12019+(﹣![]() )﹣2+
)﹣2+![]() ﹣(π﹣3.14)0
﹣(π﹣3.14)0
(4)[2(x+2y)2﹣(x+y)(4x﹣y)﹣9y2]÷(﹣2x),其中x=﹣2,y=![]() .
.
参考答案:
【答案】(1)![]() ;(2)4;(3)2+
;(2)4;(3)2+![]() ;(4)
;(4)![]()
【解析】
(1)原式先计算乘方运算,再计算单项式乘单项式法则计算即可求出值;
(2)原式变形后,利用平方差公式计算即可求出值;
(3)原式利用乘方的意义,零指数幂、负整数指数幂法则,以及二次根式性质是即可求出值;
(4)先按运算顺序把整式化简,再把对应字母的值代入求整式的值.
(1)(3ab)2(﹣![]() ab3)
ab3)
=9a2b2(![]() ab3)
ab3)
=﹣![]() ;
;
(2)20182﹣2016×2020
=20182﹣(2018﹣2)(2018+2)
=20182﹣(20182﹣4)
=4;
(3)﹣12019+(﹣![]() )﹣2+
)﹣2+![]() ﹣(π﹣3.14)0
﹣(π﹣3.14)0
=﹣1+4+2![]() ﹣1
﹣1
=2+![]() ;
;
(4)[2(x+2y)2﹣(x+y)(4x﹣y)﹣9y2]÷(﹣2x)
=[2(x2+4y2+4xy)﹣(4x2﹣xy+4xy﹣y2)﹣9y2]÷(﹣2x)
=(2x2+8y2+8xy﹣4x2+xy﹣4xy+y2﹣9y2)÷(﹣2x)
=(﹣2x2+5xy)÷(﹣2x)
=x﹣![]() y,
y,
∴当x=﹣2,y=![]() 时,原式=﹣2﹣
时,原式=﹣2﹣![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D是AB的中点,DE⊥AB,∠ACE+∠BCE=180°,EF⊥AC交AC于F,AC=12,BC=8,则AF=________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二孩政策的落实引起了全社会的关注,某校学生数学兴趣小组为了了解本校同学对父母生育二孩的态度,在学校抽取了部分同学对父母生育二孩所持的态度进行了问卷调查,调查分为非常赞同、赞同、无所谓、不赞同等四种态度.现将调查统计结果制成了如图所示的两幅统计图,请结合这两幅统计图,回答下列问题:
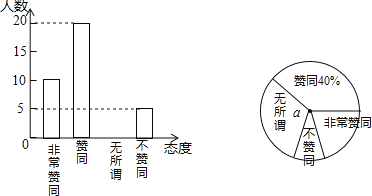
(1)在这次问卷调查中,一共抽取了 名学生,a= %;
(2)请补全条形统计图;
(3)持“不赞同”态度的学生人数的百分比所占扇形的圆心角为 °;
(4)若该校有1200名学生,请你估计该校学生对父母生育二孩持“赞同”和“非常赞同”两种态度的人数之和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【发现证明】
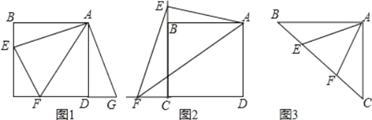
如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
【类比引申】
(1)如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;
【联想拓展】
(2)如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线和直线l在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=﹣1,P1(x1,y1),P2(x2,y2)是抛物线上的点,P3(x3,y3)是直线l上的点,且x3<﹣1<x1<x2,则y1,y2,y3的大小关系是( )

A. y1<y2<y3 B. y2<y3<y1 C. y3<y1<y2 D. y2<y1<y3
-
科目: 来源: 题型:
查看答案和解析>>【题目】按要求作图,不要求写做法,但要保留作图痕迹.
(1)如图1,四边形ABCD是平行四边形,E为BC上任意一点,请只用直尺(不带刻度)在边AD上找点F,使DF=BE.

(2)如图2,BE是菱形ABCD的边AD上的高,请只用直尺(不带刻度)作出菱形ABCD的边AB上的高DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.

(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=120°,求∠ACB的度数.
相关试题

