【题目】如图,△ABC中,D是AB的中点,DE⊥AB,∠ACE+∠BCE=180°,EF⊥AC交AC于F,AC=12,BC=8,则AF=________.

参考答案:
【答案】10
【解析】连接AE,BE,过E作EG⊥BC于G,
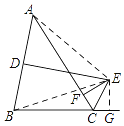
∵D是AB的中点,DE⊥AB,
∴DE垂直平分AB,
∴AE=BE,
∵∠ACE+∠BCE=180°,∠ECG+∠BCE=180°,
∴∠ACE=∠ECG,
又∵EF⊥AC,EG⊥BC,
∴EF=EG,∠FEC=∠GEC,
∵CF⊥EF,CG⊥EG,
∴CF=CG,
在Rt△AEF和Rt△BEG中,
![]() ,
,
∴Rt△AEF≌Rt△BEG(HL),
∴AF=BG,
设CF=CG=x,则AF=AC﹣CF=12﹣x,BG=BC+CG=8+x,
∴12﹣x=8+x,
解得x=2,
∴AF=12﹣2=10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,二次函数y=x2+mx+2m﹣7的图象经过点(1,0).
(1)求抛物线的表达式;
(2)把﹣4<x<1时的函数图象记为H,求此时函数y的取值范围;
(3)在(2)的条件下,将图象H在x轴下方的部分沿x轴翻折,图象H的其余部分保持不变,得到一个新图象M.若直线y=x+b与图象M有三个公共点,求b的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A,B的坐标分别为(1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD.
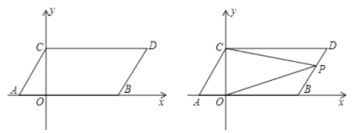
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC;
(2)在y轴上是否存在一点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由;
(3)点P是直线BD上一个动点,连接PC、PO,当点P在直线BD上运动时,请直接写出∠OPC与∠PCD、∠POB的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,点A1,B1,C1分别是BC、AC、AB的中点,A2,B2,C2分别是B1C1,A1C1,A1B1的中点,依此类推….若△ABC的周长为1,则△AnBnCn的周长为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二孩政策的落实引起了全社会的关注,某校学生数学兴趣小组为了了解本校同学对父母生育二孩的态度,在学校抽取了部分同学对父母生育二孩所持的态度进行了问卷调查,调查分为非常赞同、赞同、无所谓、不赞同等四种态度.现将调查统计结果制成了如图所示的两幅统计图,请结合这两幅统计图,回答下列问题:
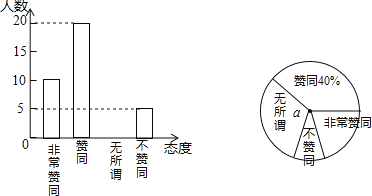
(1)在这次问卷调查中,一共抽取了 名学生,a= %;
(2)请补全条形统计图;
(3)持“不赞同”态度的学生人数的百分比所占扇形的圆心角为 °;
(4)若该校有1200名学生,请你估计该校学生对父母生育二孩持“赞同”和“非常赞同”两种态度的人数之和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【发现证明】
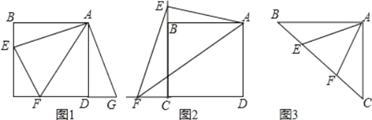
如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
【类比引申】
(1)如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;
【联想拓展】
(2)如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)(3ab)2(﹣
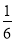 ab3)
ab3)(2)20182﹣2016×2020(利用乘法公式计算)
(3)﹣12019+(﹣
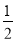 )﹣2+
)﹣2+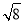 ﹣(π﹣3.14)0
﹣(π﹣3.14)0(4)[2(x+2y)2﹣(x+y)(4x﹣y)﹣9y2]÷(﹣2x),其中x=﹣2,y=
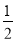 .
.
相关试题

