【题目】如图,在△ABC中,∠C=90°,AC=8,BC=6。P是AB边上的一个动点(异于A、B两点),过点P分别作AC、BC边的垂线,垂足为M、N设AP=x。

(1)在△ABC中,AB= ;
(2)当x= 时,矩形PMCN的周长是14;
(3)是否存在x的值,使得△PAM的面积、△PBN的面积与矩形PMCN的面积同时相等?请说出你的判断,并加以说明。
参考答案:
【答案】(1)10;(2)5;(3)不存在
【解析】
试题分析:(1)仔细分析题意利用勾股定理求解即可;
(2)利用MP∥BC和NP∥AC,可得到![]() ,
,![]() ,将AP=x,AB=10,BC=6,AC=8,BP=10-x
,将AP=x,AB=10,BC=6,AC=8,BP=10-x
代入式中就能得到PM和PN关于x的表达式.再由矩形周长=2(PM+PN),求出x的值.
(3)当P为AB的中点时,△PAM的面积与△PBN的面积才相等,再求出矩形PMCN的面积,进行判断.
(1)∵△ABC为直角三角形,且AC=8,BC=6,
![]()
(2))∵PM⊥AC PN⊥BC
∴MP∥BC,AC∥PN(垂直于同一条直线的两条直线平行),
∴![]() ,
,![]()
∵AP=x,AB=10,BC=6,AC=8,BP=10-x,
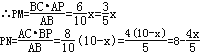
∴矩形PMCN周长=2(PM+PN)=2(![]() x+8-
x+8-![]() x)=14,解得x=5;
x)=14,解得x=5;
(3)∵PM⊥AC,PN⊥BC,
∴∠AMP=∠PNB=∠C=90.
∴AC∥PN,∠A=∠NPB.
∴△AMP∽△PNB∽△ABC.
当P为AB中点时,可得△AMP≌△PNB
此时S△AMP=S△PNB=![]() ×4×3=6
×4×3=6
而S矩形PMCN=PM·MC=3×4=12.
所以不存在x的值,能使△AMP的面积、△PNB的面积与矩形PMCN面积同时相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为1,AC,BD是对角线。将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG。则下列结论:①四边形AEGF是菱形;②△AED≌△GED;③∠DFG=112.5°;④BC+FG=1.5.其中正确的结论是( )
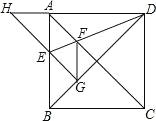
A. ①②③④ B. ①②③ C. ①② D. ②
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
 (x<0)的图象相交于点A、点B,与X轴交于点C,其中点A(﹣1,3)和点B(﹣3,n).
(x<0)的图象相交于点A、点B,与X轴交于点C,其中点A(﹣1,3)和点B(﹣3,n).(1)填空:m= ,n= .
(2)求一次函数的解析式和△AOB的面积.
(3)根据图象回答:当x为何值时,kx+b≥
 (请直接写出答案) .
(请直接写出答案) .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.

(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分10分)
如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F;再分别以点B、F为圆心,大于
 BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形. (1)根据以上尺规作图的过程,求证四边形ABEF是菱形;
(2)若菱形ABEF的周长为16,AE=4
 ,求∠C的大小.
,求∠C的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某地区30万电视观众对新闻、动画、娱乐三类节目的喜爱情况,根据老年人、成年人、青少年各年龄段实际人口的比例3:5:2,随机抽取一定数量的观众进行调查,得到如下统计图.
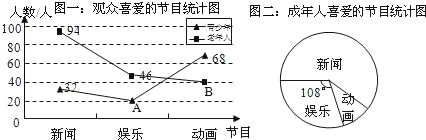
(1)上面所用的调查方法是 (填“全面调查”或“抽样调查”);
(2)写出折线统计图中A、B所代表的值和抽取观众的总人数是多少;
(3)求该地区喜爱娱乐类节目的成年人的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一病人发高烧进医院进行治疗,医生给他开了药并挂了水,同时护士每隔1小时对病人测体温,及时了解病人的好转情况,现护士对病人测体温的变化数据如下表:
时 间
7:00
8:00
9:00
10:00
11:00
12:00
13:00
14:00
15:00
体温
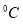 (与前一次比较)
(与前一次比较)升0.2
降1.0
降0.8
降1.0
降0.6
升0.4
降0.2
降0.2
降0
注:病人早晨进院时医生测得病人体温是40.2℃。
问:(1)病人什么时候体温达到最高,最高体温是多少?
(2)病人中午12点时体温多高?
(3)病人几点后体温稳定正常?(正常体温是37℃)
相关试题

