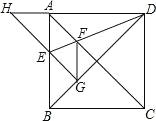
【题目】如图,正方形ABCD的边长为1,AC,BD是对角线。将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG。则下列结论:①四边形AEGF是菱形;②△AED≌△GED;③∠DFG=112.5°;④BC+FG=1.5.其中正确的结论是( )
A. ①②③④ B. ①②③ C. ①② D. ②
参考答案:
【答案】B
【解析】
首先证明△ADE≌△GDE,再求出∠AEF、∠AFE、∠GEF、∠GFE的度数,推出AE=EG=FG=AF,由此可以一一判断.
解:∵四边形ABCD是正方形,
∴AD=DC=BC=AB,∠DAB=∠ADC=∠DCB=∠ABC=90°,∠ADB=∠BDC=∠CAD=∠CAB=45°,
∵△DGH是由△DCB旋转得到,
∴DG=DC=AD,∠DGE=∠DCB=∠DAE=90°,
在Rt△AED和Rt△GED中,
![]()
∴△AED≌△GED,故②正确,
∴∠ADE=∠EDG=22.5°,AE=GE,
∴∠AED=∠AFE=67.5°,
∴AE=AF,同理GE=GF,
∴AE=GE=GF=AF,
∴四边形AEGF是菱形,故①正确,
∵∠DFG=∠GFC+∠DFC=∠BAC+∠DAC+∠ADF=112.5°,故③正确.
∵AE=FG=EG=BG,BE=![]() AE,
AE,
∴BE>AE,
∴AE<![]() ,
,
∴CB+FG<1.5,故④错误.
故选:B
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是正方形,点B,C分别在直线
 和
和 上,点A,D是x轴上两点.
上,点A,D是x轴上两点.
(1)若此正方形边长为2,k=_______.
(2)若此正方形边长为a,k的值是否会发生变化?若不会发生变化,请说明理由;若会发生变化,求出a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正比例函数y=(2m+4)x,求:
(1)m为何值时,函数图象经过第一、三象限?
(2)m为何值时,y随x的增大而减小?
(3)m为何值时,点(1,3)在该函数的图象上?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点(2,-4)在正比例函数y=kx的图象上。
(1)求k的值;
(2)若点(-1,m)在函数y=kx的图象上,试求出m的值;
(3)若A(
 ,y1),B(-2,y2),C(1,y3)都在此函数图象上,试比较y1,y2,y3的大小。
,y1),B(-2,y2),C(1,y3)都在此函数图象上,试比较y1,y2,y3的大小。 -
科目: 来源: 题型:
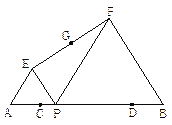
查看答案和解析>>【题目】如图:已知AB=10,点C、D在线段AB上且AC=DB=2; P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB,连结EF,设EF的中点为G;当点P从点C运动到点D时,则点G移动路径的长是________.
-
科目: 来源: 题型:
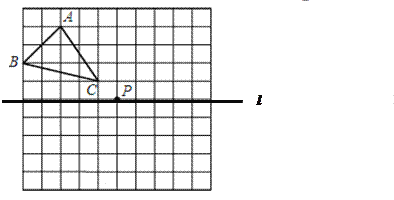
查看答案和解析>>【题目】如图,一个10×10网格,每个小正方形的边长均为1,每个小正方形的顶点叫格点,△ABC的顶点均在格点上.
(1)画出△ABC关于直线l的对称的△A1B1C1.
(2)画出△ABC关于点P的中心对称图形△A2B2C2.
(3)△A1B1C1与△A2B2C2组成的图形_______________(是或否)轴对称图形,如果是轴对称图形,请画出对称轴.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.

(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
相关试题

