Question

【题目】在△ABC中，D为BC边上一点．

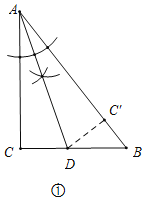
(1)如图①，在Rt△ABC中，∠C＝90°，将△ABC沿着AD折叠，点C落在AB边上．请用直尺和圆规作出点D（不写作法，保留作图痕迹）；

(2)如图②，将△ABC沿着过点D的直线折叠，点C落在AB边上的E处．

①若DE⊥AB，垂足为E，请用直尺和圆规作出点D（不写作法，保留作图痕迹）；

②若AB＝，BC＝3，∠B＝45°，求CD的取值范围．

Answer 1

【答案】（1）详见解析；（2）详见解析；（3）

【解析】试题分析：（1）作∠CAB的角平分线即可；

（2）①过点C作CE⊥BC，交BA的延长线于E，作∠CEB的角平分线即可；

②在如图②中，求出CD的最小值，在如图③当E与A重合时，作AH⊥CB于H，设CD=DE=x，求出CD可得CD的最大值．

试题解析：解：（1）点D如图所示．（作∠CAB的角平分线即可）

（2）①点D如图所示．（过点C作CE⊥BC，交BA的延长线于E，作∠CEB的角平分线即可）

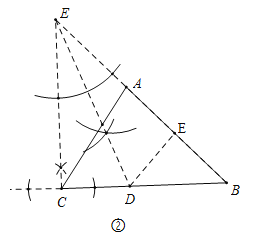
②如图②中，设CD=DE=x，则DE=EB=x，∠DEB=90°，DB=x，∵BC=3，∴x+x=3，∴x=，如图③中，当E与A重合时，作AH⊥CB于H，设CD=DE=x，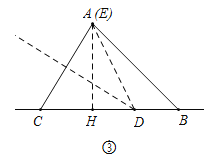

在Rt△AHB中，易知AH=HB=2，∠AHB=90°，HD=x﹣1，DE=x，∴x2=22+（x﹣1）2，∴x= ．

综上可知，CD的最大值为，最小值为，∴≤CD≤，故答案为： ≤CD≤．