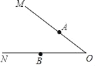
【题目】如图,已知∠MON,点A,B分别在OM,ON边上,且OA=OB.
(1)求作:过点A,B分别作OM,ON的垂线,两条垂线的交点记作点D(保留作图痕迹,不写作法);
(2)连接OD,若∠MON=50°,则∠ODB= °.
参考答案:
【答案】(1)见解析;(2)65.
【解析】
(1)根据过直线上一点作直线垂线的方法作出垂线即可;
(2)利用全等三角形的判定与性质结合四边形内角和定理得出答案.
解:(1)如图,DA,DB即为所求垂线;
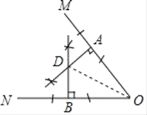
(2)连接OD,
∵DB⊥ON,DA⊥OM,
∴∠OBD=∠OAD=90°,∠MON=50°,
∴∠ADB=180°﹣50°=130°.
在Rt△OBD与Rt△OAD中,
∵![]() ,
,
∴Rt△OBD≌Rt△OAD(HL),
∴∠ODB=![]() ∠ADB=65°.
∠ADB=65°.
故答案为:65.
-
科目: 来源: 题型:
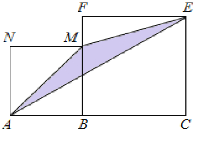
查看答案和解析>>【题目】如图,点B在线段AC上(BC>AB),在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为S3;则S2020﹣S2019=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数
 图象的一部分,对称轴为
图象的一部分,对称轴为  ,且经过点(2,0)下列说法:①abc<0;②-2b+c=0;③4a+2b+c<0;④若(-
,且经过点(2,0)下列说法:①abc<0;②-2b+c=0;③4a+2b+c<0;④若(-  ,y1),(
,y1),(  ,y2)是抛物线上的两点,则y1<y2;⑤
,y2)是抛物线上的两点,则y1<y2;⑤ 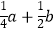 >m(am+b)其中(m≠
>m(am+b)其中(m≠  )其中说法正确的是( )
)其中说法正确的是( )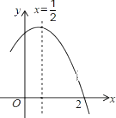
A.①②④⑤
B.③④
C.①③
D.①②⑤ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=BC=
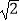 ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B=
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B=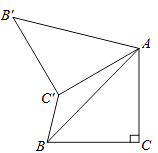
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F,且AD=CD.
(1)求证:△ABD≌△CFD;
(2)已知BC=7,AD=5,求AF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系网格中,△ABC的顶点都在格点上,点C坐标(0,-1).

(1)①作出△ABC 关于原点对称的△A1B1C1 , 并写出点A1的坐标;
②把△ABC 绕点C逆时针旋转90°,得△A2B2C2 , 画出△A2B2C2 , 并写出点A2的坐标;
(2)直接写出△A2B2C2的面积 -
科目: 来源: 题型:
查看答案和解析>>【题目】山地自行车越来越受中学生的喜爱.一网店经营的一个型号山地自行车,今年一月份销售额为30000元,二月份每辆车售价比一月份每辆车售价降价100元,若销售的数量与上一月销售的数量相同,则销售额是27000元.
(1)求二月份每辆车售价是多少元?
(2)为了促销,三月份每辆车售价比二月份每辆车售价降低了10%销售,网店仍可获利35%,求每辆山地自行车的进价是多少元?
相关试题

