【题目】如图是二次函数 ![]() 图象的一部分,对称轴为
图象的一部分,对称轴为 ![]() ,且经过点(2,0)下列说法:①abc<0;②-2b+c=0;③4a+2b+c<0;④若(-
,且经过点(2,0)下列说法:①abc<0;②-2b+c=0;③4a+2b+c<0;④若(- ![]() ,y1),(
,y1),( ![]() ,y2)是抛物线上的两点,则y1<y2;⑤
,y2)是抛物线上的两点,则y1<y2;⑤ ![]() >m(am+b)其中(m≠
>m(am+b)其中(m≠ ![]() )其中说法正确的是( )
)其中说法正确的是( )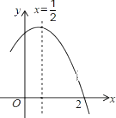
A.①②④⑤
B.③④
C.①③
D.①②⑤
参考答案:
【答案】A
【解析】根据抛物线开口方向及与y轴的交点的位置,可知a<0,c>0,根据对称轴的位置在y轴的右侧,由“左同右异”可知a、b异号,得出b>0,abc<0,故①正确;
根据抛物线的对称轴为直线x=-![]() =
=![]() 得出a=-b①,因为x=2时y=0.得4a+2b+c=0②,将①代入②得-2b+c=0,故②正确;
得出a=-b①,因为x=2时y=0.得4a+2b+c=0②,将①代入②得-2b+c=0,故②正确;
根据x-2时y=0得出4a+2b+c=0,故③错误;
∵点(-![]() ,y1)离对称轴要比(
,y1)离对称轴要比( ![]() ,y2)离对称轴远,∴y1<y2,故④正确;
,y2)离对称轴远,∴y1<y2,故④正确;
当x=![]() 时,y有最大值,所以
时,y有最大值,所以 ![]() a +
a + ![]() b+c>am2+bm+c(m≠
b+c>am2+bm+c(m≠ ![]() ),即
),即 ![]() a +
a + ![]() b>m(am+b)(m≠
b>m(am+b)(m≠ ![]() )。故⑤正确。
)。故⑤正确。
根据抛物线开口方向及与y轴的交点的位置,可知a<0,c>0,根据对称轴的位置在y轴的右侧,由“左同右异”可知a、b异号。得出b>0 ,即可对①作出判断;根据抛物线的对称轴得出a=-b,再结合x=2时y=0,即可对②作出判断;根据x-2时y=0得出4a+2b+c=0,即可对③作出判断;根据二次函数的性质可对④作出判断;根据二次函数的性质,当x=![]() ,y有最大值,可对⑤作出判断。从而得出正确选项。
,y有最大值,可对⑤作出判断。从而得出正确选项。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:抛物线
 经过坐标原点,且当
经过坐标原点,且当  时, y随x的增大而减小.
时, y随x的增大而减小.
(1)求抛物线的解析式;
(2)如下图,设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB x轴于点B, DC
x轴于点B, DC  x轴于点C.
x轴于点C.
①当 BC=1时,直接写出矩形ABCD的周长;
②设动点A的坐标为(a, b),将矩形ABCD的周长L表示为a的函数,并写出自变量的取值范围,判断周长是否存在最大值,如果存在,求出这个最大值,并求出此时点A的坐标;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.

下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.
其中合理的是( )
A.①
B.②
C.①②
D.①③ -
科目: 来源: 题型:
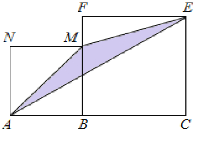
查看答案和解析>>【题目】如图,点B在线段AC上(BC>AB),在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为S3;则S2020﹣S2019=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=BC=
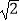 ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B=
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B=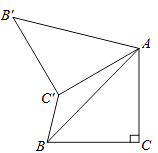
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MON,点A,B分别在OM,ON边上,且OA=OB.
(1)求作:过点A,B分别作OM,ON的垂线,两条垂线的交点记作点D(保留作图痕迹,不写作法);
(2)连接OD,若∠MON=50°,则∠ODB= °.
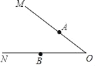
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F,且AD=CD.
(1)求证:△ABD≌△CFD;
(2)已知BC=7,AD=5,求AF的长.

相关试题

