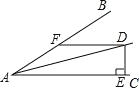
【题目】如图∠BAC=30°,D 为角平分线上一点,DE⊥AC 于 E,DF∥AC且交AB于F.
(1)求证:△ADF 是等腰三角形.
(2)若 DF=10cm,求 DE的长.
参考答案:
【答案】(1)证明见解析;(2)5cm.
【解析】
(1)根据角平分线的定义、平行线的性质、等腰三角形的判定定理证明;
(2)作DH⊥AB于H,根据直角三角形的性质求出BH,根据角平分线的性质定理解答.
(1)证明:∵∠BAC=30°,D为角平分线上一点,
∴∠BAD=∠CAD,
∵DF∥AC,
∴∠CAD=∠FDA,
∴∠BAD=∠FDA,
∴FA=FD,即△ADF是等腰三角形;
(2)解:作DH⊥AB于H,
∵DF∥AC,
∴∠BFD=∠BAC=30°,
∴DH=![]() DF=5,
DF=5,
∵D为角平分线上一点,DE⊥AC,DH⊥AB,
∴DE=DH=5cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究题:
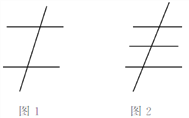
(1)如图1,两条水平的直线被一条竖直的直线所截,同位角有__________对,内错角有__________对,同旁内角有__________对;
(2)如图2,三条水平的直线被一条竖直的直线所截,同位角有__________对,内错角有__________对,同旁内角有__________对;
(3)根据以上探究的结果,n(n为大于1的整数)条水平直线被一条竖直直线所截,同位角有__________对,内错角有__________对,同旁内角有__________对.(用含n的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知正比例函数y=
 x的图象与反比例函数y=
x的图象与反比例函数y= 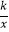 的图象交于A(a,﹣2),B两点.
的图象交于A(a,﹣2),B两点. 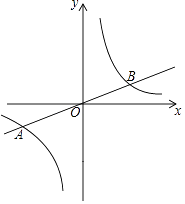
(1)求反比例函数的表达式和点B的坐标;
(2)P是第一象限内反比例函数图象上一点,过点P作y轴的平行线,交直线AB于点C,连接PO,若△POC的面积为3,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
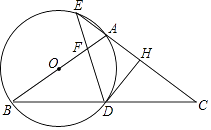
(1)求证:DH是圆O的切线;
(2)若A为EH的中点,求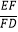 的值;
的值;
(3)若EA=EF=1,求圆O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,F为CD上一点,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度数为整数,则∠C的度数为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;
(1)直接写出图中∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.

-
科目: 来源: 题型:
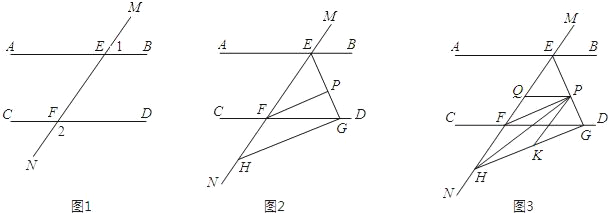
查看答案和解析>>【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.
相关试题

