【题目】综合与探究
如图1,在平面直角坐标系中,点![]() 是坐标原点,点
是坐标原点,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 的坐标为
的坐标为![]() ,四边形
,四边形![]() 是菱形,直线
是菱形,直线![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.

(1)点![]() 的坐标是______;
的坐标是______;
(2)求直线![]() 的函数解析式;
的函数解析式;
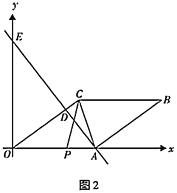
(3)如图2,动点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 方向以1个单位长度/秒的速度向终点
方向以1个单位长度/秒的速度向终点![]() 匀速运动,设
匀速运动,设![]() 的面积为
的面积为![]() (
(![]() ),点
),点![]() 的运动时间为
的运动时间为![]() 秒,求
秒,求![]() 与
与![]() 之间的函数关系式(要求写出自变量
之间的函数关系式(要求写出自变量![]() 的取值范围)
的取值范围)
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
![]() 或
或![]()
![]() .
.
【解析】
(1)由点C坐标求OC的长,得到菱形边长为5,再根据CB∥x轴且CB=OC=5,即求出点B坐标;
(2)过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 轴,由点C的坐标求出OF,CF的长,然后证得
轴,由点C的坐标求出OF,CF的长,然后证得![]() ,得出OD,AD的长,根据三角形的面积求出DH,再根据勾股定理求得OH,即可得点D坐标,然后利用待定系数法求得AD的解析式;
,得出OD,AD的长,根据三角形的面积求出DH,再根据勾股定理求得OH,即可得点D坐标,然后利用待定系数法求得AD的解析式;
(3)由点P在折线OAB上运动可知需分两种情况讨论.当点![]() 在
在![]() 边上运动时,根据
边上运动时,根据![]() 即可得出S与t的关系式;当点
即可得出S与t的关系式;当点![]() 在
在![]() 边上运动时,过点
边上运动时,过点![]() 作
作![]() ,可得
,可得![]() .根据
.根据![]() 即可得出S与t的关系式.
即可得出S与t的关系式.
解:(1)过点C作CF⊥x轴于点F,

∴∠CFO=90°
∵点C的坐标为(4,3),
∴OF=4,CF=3
∴OC=![]() =
=![]() =5,
=5,
∵四边形OABC是菱形,
∴OA=BC=OC=5,BC∥x轴,
∴yB=yC=3,xB=xC+5=9,
故答案为:(9,3);
(2)如答图1,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,

∵点![]() 的坐标为
的坐标为![]() ,∴
,∴![]() ,
,![]() .
.
∴![]() .
.
∵四边形![]() 为菱形,
为菱形,
∴![]() .
.
∴![]() .
.
在![]() 和
和![]() 中,
中,

∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
∴ .
.
∴![]() .
.
设直线![]() 的函数解析式为
的函数解析式为![]() .
.
∵
解得
∴直线![]() 的函数解析式为
的函数解析式为![]() .
.
(3)分两种情况:
①当点![]() 在
在![]() 边上运动时,
边上运动时,
∴![]()
![]() .
.
②如答图2,当点![]() 在
在![]() 边上运动时,
边上运动时,
由(2)得![]() ,
,
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
∴![]() .
.
∴![]()
![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“春种一粒粟,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物.我省有着“小杂粮王国”的美誉,谷子是我省杂粮谷物中的大类.某小米经销商要将规格相同的1000袋小米运往
 ,
, ,
, 三地销售,要求运往
三地销售,要求运往 地的袋数是运往
地的袋数是运往 地袋数的3倍,各地的运费如下表所示:
地袋数的3倍,各地的运费如下表所示:运往地
 地
地 地
地 地
地运费(元/袋)
20
10
15

(1)设运往
 地的小米为
地的小米为 (袋),总运费为
(袋),总运费为 (元),试写出
(元),试写出 与
与 的函数关系式;
的函数关系式;(2)若总运费不超过14000元,最多可运往
 地多少袋小米?
地多少袋小米? -
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践
问题情境:如图1,在正方形
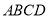 中,点
中,点 是对角线
是对角线 上的一点,点
上的一点,点 在
在 的延长线上,且
的延长线上,且 ,
, 交
交 于点
于点 .问题解决:
.问题解决:
(1)求证:
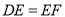 ;
;(2)求
 的度数;
的度数;探索发现:
(3)如图2,若点
 在边
在边 上,且
上,且 ,求
,求 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形ABC的三边长分别为6 cm、7.5 cm、9 cm,三角形DEF的一边长为4 cm.当三角形DEF的另两边长是下列哪一组时,这两个三角形相似( )
A. 2 cm、3 cm B. 4 cm、5 cm C. 5 cm、6 cm D. 6 cm、7 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△DEF中,∠ACB=∠EFD=90°,点B、F、C、D在同一直线上,已知AB⊥DE,且AB=DE,AC=6,EF=8,DB=10,则CF的长度为___________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个装有A、B两个阀门的空容器,打开A阀门水将匀速注入甲容器,打开B阀门甲容器的水将匀速注入乙容器(水流动过程的时间忽略不计),小溪先打开A阀门,几分钟后再打开B阀门,甲、乙两容器内水的体积的差值y(升)和小溪打开A阀门的时间x(分钟)之间的关系如图2所示,则图2中转折点P对应的时间是___________分钟.

-
科目: 来源: 题型:
查看答案和解析>>【题目】6月18日晚,苏宁易购发布618全程战报:从6月1日到18日晚6点,苏宁依托线上线下全场景优势,逆势增长.经调查,苏宁易购线上有甲乙两家在销售华为A手机、华为B电脑和华为C耳机.已知每部A手机的利润率为40%,每台B电脑的利润率为60%,每副C耳机的利润率为30%,甲商家售出的B电脑和C耳机的数量都是A手机的数量的一半,获得的总利润为50%,乙商家售出的A手机的数量是B电脑的数量的一半,售出的C耳机的数量是B电脑的数量的
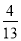 ,则乙商家获得的总利润率是___________.
,则乙商家获得的总利润率是___________.
相关试题

