【题目】如图,在ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/s秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动,点P运动到F点时停止运动,点Q也同时停止运动,当点P运动__秒时,以P、Q、E、F为顶点的四边形是平行四边形.

参考答案:
【答案】3或5
【解析】
由四边形ABCD是平行四边形得出:AD∥BC,AD=BC,∠ADB=∠CBD,又由∠FBM=∠CBM,即可证得FB=FD,求出AD的长,得出CE的长,设当点P运动t秒时,点P、Q、E、F为顶点的四边形是平行四边形,根据题意列出方程并解方程即可得出结果.
解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ADB=∠CBD,
∵∠FBM=∠CBM,
∴∠FBD=∠FDB,
∴FB=FD=12cm,
∵AF=6cm,
∴AD=18cm,
∵点E是BC的中点,
∴CE=![]() BC=
BC=![]() AD=9cm,
AD=9cm,
要使点P、Q、E、F为顶点的四边形是平行四边形,则PF=EQ即可,
设当点P运动t秒时,点P、Q、E、F为顶点的四边形是平行四边形,
根据题意得:6-t=9-2t或6-t=2t-9,
解得:t=3或t=5.
故答案为:3或5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,点
中,点 ,
, 分别在边
分别在边 ,
, 上,有下列条件:
上,有下列条件:①
 ;②
;② ;③
;③ ;④
;④ .其中,能使四边形
.其中,能使四边形 是平行四边形的条件有( ).
是平行四边形的条件有( ).
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF=
 ;④S△AEF=
;④S△AEF= .其中正确的有( )
.其中正确的有( )
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将某点(横坐标与纵坐标不相等)的横坐标与纵坐标互换后得到的点叫这个点的“互换点”,如(-3,5)与(5,-3)是一对“互换点”.
(1)以O为圆心,半径为5的圆上有无数对“互换点”,请写出一对符合条件的“互换点”;
(2)点M,N是一对“互换点”,点M的坐标为(m,n),且(m>n),⊙P经过点M,N.
①点M的坐标为(4,0),求圆心P所在直线的表达式;
②⊙P的半径为5,求m-n的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】结合数轴与绝对值的知识回答下列问题:

(1)数轴上表示
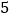 和
和 的两点之间的距离是__________;表示
的两点之间的距离是__________;表示 和
和 两点之间的距离是__________;
两点之间的距离是__________;(2)如果
 ,那么
,那么 __________;
__________;(3)若
 ,
, ,且数
,且数 、
、 在数轴上表示的点分别是点
在数轴上表示的点分别是点 、点
、点 ,则
,则 、
、 两点间的最大距离是_____,最小距离是______;
两点间的最大距离是_____,最小距离是______;(4)求代数式
 的最小值,并写出此时
的最小值,并写出此时 可取哪些整数值?
可取哪些整数值?(5)求代数式
 的最小值.
的最小值.(6)若
 表示一个有理数,则代数式
表示一个有理数,则代数式 有最大值吗?若有,请求出最大值;若没有,请说明理由.
有最大值吗?若有,请求出最大值;若没有,请说明理由. -
科目: 来源: 题型:
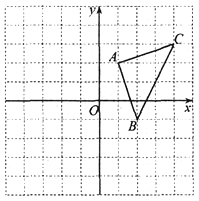
查看答案和解析>>【题目】如图,平面直角坐标系中,△ABC的顶点坐标为:A(1,2),B(2, 一1), C (4, 3).
(1)将△ABC向左平移2个单位长度,再向上平移1个单位长度,得△A'B'C'.画出△A'B'C',并写出△A'B'C'的顶点坐标;
(2)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解决问题:
一辆货车从超市出发,向东走了3千米到达小彬家,继续走2.5千米到达小颖家,然后向西走了10千米到达小明家,最后回到超市.
(1)以超市为原点,以向东的方向为正方向,用1个单位长度表示1千米,在数轴上表示出小明家,小彬家,小颖家的位置.
(2)小明家距小彬家多远?
(3)货车一共行驶了多少千米?
(4)货车每千米耗油0.2升,这次共耗油多少升?
相关试题

