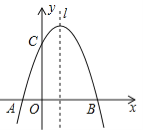
【题目】如图,已知抛物线![]() 与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0)
与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0)
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
参考答案:
【答案】(1) m=2,顶点坐标为:(1,4);(2)(1,2).
【解析】(1)把点B的坐标为(3,0)代入抛物线![]() 得:
得:![]() ,解得:m=2,∴
,解得:m=2,∴![]() =
=![]() ,∴顶点坐标为:(1,4).
,∴顶点坐标为:(1,4).
(2)连接BC交抛物线对称轴l于点P,则此时PA+PC的值最小,设直线BC的解析式为:y=kx+b,∵点C(0,3),点B(3,0),∴![]() ,解得:
,解得:![]() ,∴直线BC的解析式为:y=﹣x+3,当x=1时,y=﹣1+3=2,∴当PA+PC的值最小时,求点P的坐标为:(1,2).
,∴直线BC的解析式为:y=﹣x+3,当x=1时,y=﹣1+3=2,∴当PA+PC的值最小时,求点P的坐标为:(1,2).

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,以点(﹣3,4)为圆心,4为半径的圆( )
A.与x轴相交,与y轴相切
B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交
D.与x轴相切,与y轴相离 -
科目: 来源: 题型:
查看答案和解析>>【题目】如下图。

(1)观察发现:如图1,已知Rt△ABC,∠ABC=90°,分别以AB,BC为边,向外作正方形ABDE和正方形BCFG,连接DG.若M是DG的中点,不难发现:BM= AC.
AC.
请完善下面证明思路:①先根据 ,证明BM=
,证明BM=  DG;②再证明
DG;②再证明  ,得到DG=AC;所以BM=
,得到DG=AC;所以BM=  AC;
AC;
(2)数学思考:若将上题的条件改为:“已知Rt△ABC,∠ABC=90°,分别以AB,AC为边向外作正方形ABDE和正方形ACHI,N是EI的中点”,则相应的结论“AN= BC”成立吗?小颖通过添加如图2所示的辅助线验证了结论的正确性.请写出小颖所添加的辅助线的作法,并由此证明该结论;
BC”成立吗?小颖通过添加如图2所示的辅助线验证了结论的正确性.请写出小颖所添加的辅助线的作法,并由此证明该结论;
(3)拓展延伸:如图3,已知等腰△ABC和等腰△ADE,AB=AC,AD=AE.连接BE,CD,若P是CD的中点,探索:当∠BAC与∠DAE满足什么条件时,AP= BE,并简要说明证明思路.
BE,并简要说明证明思路.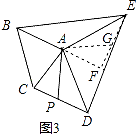
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一台装有30升柴油的柴油机,工作时平均每小时耗油3升,请写出柴油机剩余油量Q关于时间t的函数关系式_________(不要求写定义域)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解学校开展“孝敬父母,从家务事做起”活动的实施情况,该校抽取八年级5名学生调查他们一周(按7天计算)做家务所用时间(单位:小时,调查结果保留一位小数),得到一组数据,并绘制成统计表,请根据表完成下列各题:
分组
划记
频数
频率
0.55~1.05
正正…
14
0.28
1.05~1.55
正正正
15
0.30
1.55~2.05
正…
7
2.05~2.55
…
4
0.08
2.55~3.05
…
5
0.10
3.05~3.55
…
3
3.55~4.05
T
0.04
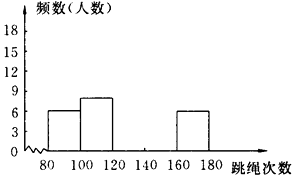
(1)填写频率分布表中末完成的部分.
(2)由以上信息判断,每周做家务的时间不超过1.55h的学生所占的百分比是 .
(3)针对以上情况,写一个20字以内倡导“孝敬父母,热爱劳动”的句子. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=x2﹣mx+m﹣2
(1)求证:无论m为任何实数,该二次函数的图象与x轴都有两个交点;
(2)若图象经过原点,求二次函数的解析式.
-
科目: 来源: 题型:
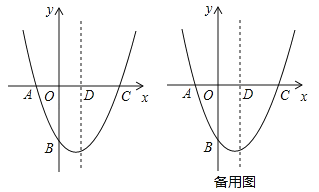
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数
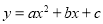 的图象经过点A(﹣1,0),B(0,
的图象经过点A(﹣1,0),B(0,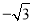 ),C(2,0),其对称轴与x轴交于点D.
),C(2,0),其对称轴与x轴交于点D.(1)求二次函数的表达式及其顶点坐标;
(2)若P为y轴上的一个动点,连接PD,则
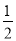 PB+PD的最小值为 ;
PB+PD的最小值为 ;(3)M(x,t)为抛物线对称轴上一动点.
①若平面内存在点N,使得以A,B,M,N为顶点的四边形为菱形,则这样的点N共有 个;
②连接MA,MB,若∠AMB不小于60°,求t的取值范围.
相关试题

