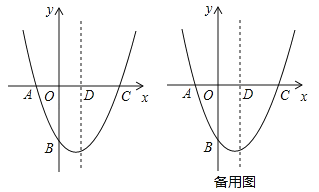
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象经过点A(﹣1,0),B(0,
的图象经过点A(﹣1,0),B(0,![]() ),C(2,0),其对称轴与x轴交于点D.
),C(2,0),其对称轴与x轴交于点D.
(1)求二次函数的表达式及其顶点坐标;
(2)若P为y轴上的一个动点,连接PD,则![]() PB+PD的最小值为 ;
PB+PD的最小值为 ;
(3)M(x,t)为抛物线对称轴上一动点.
①若平面内存在点N,使得以A,B,M,N为顶点的四边形为菱形,则这样的点N共有 个;
②连接MA,MB,若∠AMB不小于60°,求t的取值范围.
参考答案:
【答案】(1)![]() ,顶点坐标(
,顶点坐标(![]() ,
,![]() );(2)
);(2)![]() ;(3)①5;②
;(3)①5;②![]() ≤t≤
≤t≤![]() .
.
【解析】(1)由题意得: ,解得:
,解得: ,∴抛物线解析式为
,∴抛物线解析式为![]() ,∵
,∵![]() =
=![]() ,∴顶点坐标(
,∴顶点坐标(![]() ,
,![]() ).
).
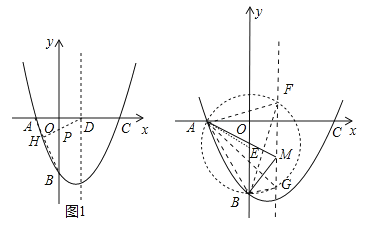
(2)如图1中,连接AB,作DH⊥AB于H,交OB于P,此时![]() PB+PD最小.
PB+PD最小.
理由:∵OA=1,OB=![]() ,∴tan∠ABO=
,∴tan∠ABO=![]() ,∴∠ABO=30°,∴PH=
,∴∠ABO=30°,∴PH=![]() PB,∴
PB,∴![]() PB+OD=PH+PD=DH,∴此时
PB+OD=PH+PD=DH,∴此时![]() PB+PD最短(垂线段最短).
PB+PD最短(垂线段最短).
在RT△ADH中,∵∠AHD=90°,AD=![]() ,∠HAD=60°,∴sin60°=
,∠HAD=60°,∴sin60°=![]() ,∴DH=
,∴DH=![]() ,∴
,∴![]() PB+PD的最小值为
PB+PD的最小值为![]() .故答案为:
.故答案为:![]() .
.
(3)①以A为圆心AB为半径画弧与对称轴有两个交点,以B为圆心AB为半径画弧与对称轴也有两个交点,线段AB的垂直平分线与对称轴有一个交点,所以满足条件的点M有5个,即满足条件的点N也有5个,故答案为:5.
②如图,RT△AOB中,∵tan∠ABO=![]() ,∴∠ABO=30°,作AB的中垂线与y轴交于点E,连接EA,则∠AEB=120°,以E为圆心,EB为半径作圆,与抛物线对称轴交于点F、G.
,∴∠ABO=30°,作AB的中垂线与y轴交于点E,连接EA,则∠AEB=120°,以E为圆心,EB为半径作圆,与抛物线对称轴交于点F、G.
则∠AFB=∠AGB=60°,从而线段FG上的点满足题意,∵EB=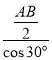 =
=![]() ,∴OE=OB﹣EB=
,∴OE=OB﹣EB=![]() ,∵F(
,∵F(![]() ,t),
,t),![]() ,∴
,∴![]() ,解得t=
,解得t=![]() 或
或![]() ,故F(
,故F(![]() ,
,![]() ),G(
),G(![]() ,
,![]() ),∴t的取值范围
),∴t的取值范围![]() ≤t≤
≤t≤![]()
-
科目: 来源: 题型:
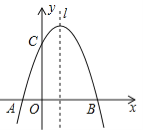
查看答案和解析>>【题目】如图,已知抛物线
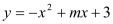 与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0)
与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0)(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解学校开展“孝敬父母,从家务事做起”活动的实施情况,该校抽取八年级5名学生调查他们一周(按7天计算)做家务所用时间(单位:小时,调查结果保留一位小数),得到一组数据,并绘制成统计表,请根据表完成下列各题:
分组
划记
频数
频率
0.55~1.05
正正…
14
0.28
1.05~1.55
正正正
15
0.30
1.55~2.05
正…
7
2.05~2.55
…
4
0.08
2.55~3.05
…
5
0.10
3.05~3.55
…
3
3.55~4.05
T
0.04
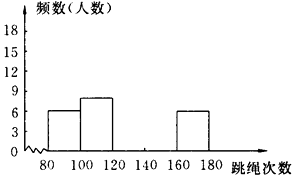
(1)填写频率分布表中末完成的部分.
(2)由以上信息判断,每周做家务的时间不超过1.55h的学生所占的百分比是 .
(3)针对以上情况,写一个20字以内倡导“孝敬父母,热爱劳动”的句子. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=x2﹣mx+m﹣2
(1)求证:无论m为任何实数,该二次函数的图象与x轴都有两个交点;
(2)若图象经过原点,求二次函数的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个非零有理数和它的相反数相乘之积一定是。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,对称轴为直线x=
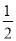 的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A.
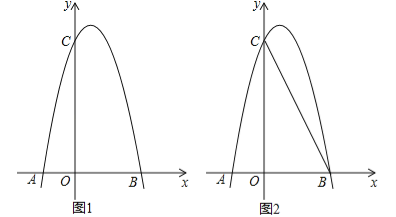
的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A.(1)求抛物线的解析式;
(2)若点P为第一象限内抛物线上的一点,设四边形COBP的面积为S,求S的最大值;
(3)如图2,若M是线段BC上一动点,在x轴是否存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上A点表示原点左边距离原点3个单位长度、B点在原点右边距离原点2个单位长度,那么两点所表示的有理数的积是。
相关试题

