【题目】已知:如图①,直线MN⊥直线PQ,垂足为O,点A在射线OP上,点B在射线OQ上(A、B不与O点重合),点C在射线ON上且OC=2,过点C作直线![]() ∥PQ,点D在点C的左边且CD=3.
∥PQ,点D在点C的左边且CD=3.
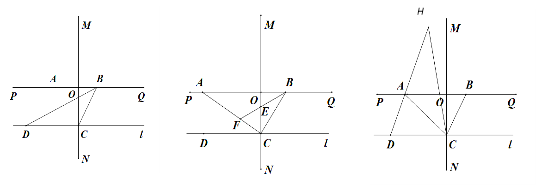
(1) 直接写出△BCD的面积.
(2) 如图②,若AC⊥BC,作∠CBA的平分线交OC于E,交AC于F,则∠CEF与∠CFE有何数量关系?请说明理由.
(3) 如图③,若∠ADC=∠DAC,点B在射线OQ上运动,∠ACB的平分线交DA的延长线于点H,在点B运动过程中![]() 的值是否变化?若不变,直接写出其值;若变化,直接写出变化范围.
的值是否变化?若不变,直接写出其值;若变化,直接写出变化范围.
参考答案:
【答案】(1)、3;(2)、∠CEF=∠CFE;(3)、![]()
【解析】
试题分析:(1)、根据三角形的面积计算公式求出三角形的面积;(2)、根据垂直得出∠BCO=∠BAC,根据角平分线得出∠ABF=∠CBF,则∠ABF+∠BAC=∠CBF+∠BCO,根据△ABF和△BCE的内角和定理得出∠AFB=∠CEB,从而得出答案;(3)、根据题意求出![]() 的大小.
的大小.
试题解析:(1)、S△BCD=3
(2)、∠CEF=∠CFE
理由:∵AC⊥BC,MN⊥AB ∴∠BAC+∠ABC=90°,∠BCO+∠ABC=90°, ∴∠BCO+∠ABC=∠BAC+∠ABC,
∴∠BCO =∠BAC, ∵BF平分∠CBA ∴∠ABF=∠CBF ∴∠ABF+∠BAC =∠CBF+∠BCO
在△ABF与△BCE中 ∠ABF+∠BAC +∠AFB =∠CBF+∠BCA+∠CEB=1800
∴∠AFB=∠CEB ∴∠CEF=∠CFE
(3)、![]() =
=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】等边三角形的边长为a,则它的周长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨2元,就会少售出20件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润ω元,并把结果填写在表格中:
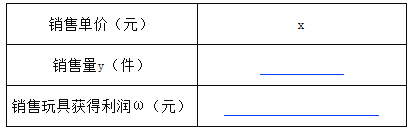
(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元?
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于400件的销售任务,求商场销售该品牌玩具获得的最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两辆汽车同时分别从A、B两城沿同一条高速公路匀速驶向C城.已知A、C两城的距离为360km,B、C两城的距离为320km,甲车比乙车的速度快10km/h,结果两辆车同时到达C城.设乙车的速度为xkm/h.
(1)根据题意填写下表:
行驶的路程(km)
速度(km/h)
所需时间(h)
甲车
360
乙车
320
x
(2)求甲、乙两车的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个等腰三角形静的两边长分别为5或6,则这个等腰三角形的周长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中有两点M(a,b),N(c,d),规定(a,b)⊕(c,d)=(a+c,b+d),则称点Q(a+c,b+d)为M,N的“和点”.若以坐标原点O与任意两点及它们的“和点”为顶点能构成四边形,则称这个四边形为“和点四边形”,现有点A(2,5),B(﹣1,3),若以O,A,B,C四点为顶点的四边形是“和点四边形”,则点C的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC与△DEF相似且面积之比为25:16,则△ABC与△DEF的周长之比为 .
相关试题

