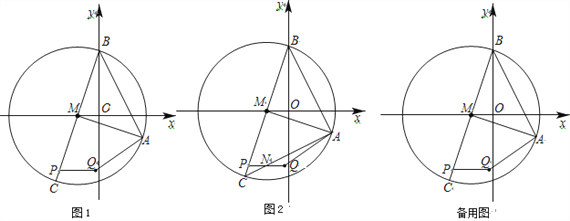
【题目】已知:如图1,在平面直角坐标系中,A(2,-1),以M(-1,0)为圆心,以AM为半径的圆交y轴于点B,连结BM并延长交⊙M于点C,动点P在线段BC上运动,长为![]() 的线段PQ∥x轴(点Q在点P右侧),连结AQ.
的线段PQ∥x轴(点Q在点P右侧),连结AQ.
(1)求⊙M的半径长和点B的坐标;
(2)如图2,连结AC,交线段PQ于点N,
①求AC所在直线的解析式;
②当PN=QN时,求点Q的坐标;
(3)点P在线段BC上运动的过程中,请直接写出AQ的最小值和最大值.
参考答案:
【答案】(1)半径为![]() ,点B(0,3);
,点B(0,3);
(2)①yAC=![]() x-2,②点Q坐标为(-
x-2,②点Q坐标为(-![]() ,-
,- ![]() )
)
(3)AQ最小值为![]() ,AQ最大值为
,AQ最大值为![]()
【解析】试题分析:(1)、过点A作AE⊥x轴,则AE=1,ME=3,从而得出圆的半径,然后根据Rt△MOB的勾股定理得出OB的长度,得出点B的坐标;(2)、首先设直线AC的解析式为:y=kx+b,根据中心对称的性质得出点C的坐标,利用待定系数法求出函数解析式;根据题意得出直线BC的解析式为y=3x+3,设点P的坐标为(x,3x+3),从而得出点N的坐标,然后根据点N在直线AC上求出x的值,从而得出点Q的坐标;(3)、根据最小值和最大值的计算法则以及勾股定理得出最值.
试题解析:(1)过点A作AE⊥x轴,则AE=1,ME=3,∴AM=![]() ,即半径为
,即半径为![]()
所以BM=![]() ,∵OM=1,∴OB=3,即点B(0,3)
,∵OM=1,∴OB=3,即点B(0,3)
(2)①设解析式为设yAC=kx+b 由题意得点C与点B关于点M成中心对称,
∴点C(-2,-3) 又点A(2,-1)
即当x=2时,y=-1;当x=-2时,y=-3 解得k=![]() ,b=-2 ∴yAC=
,b=-2 ∴yAC=![]() x-2
x-2
②可求yBC=3x+3,设点P(x,3x+3) 由题意得点N为(x+![]() ,3x+3)
,3x+3)
∵点N落在AC上,所以3x+3=![]() ( x+
( x+![]() )-2 解得x=-
)-2 解得x=-![]()
所以点Q坐标为(-![]() ,-
,-![]() )
)
(3)AQ最小值为![]() , AQ最大值为
, AQ最大值为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组﹣1<x<4的整数解有_________个.
-
科目: 来源: 题型:
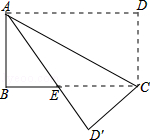
查看答案和解析>>【题目】如图所示,四边形ABCD是矩形,把△ACD沿AC折叠到△ACD′,AD′与BC交于点E,若AD=4,DC=3,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式由左边到右边的变形中,属于因式分解的是( )
A.x2﹣2x+2=x(x﹣2)+2
B.(x+y)(x﹣y)=x2﹣y2
C.(2a﹣b)2=4a2﹣4ab+b2
D.x2+4x+4=(x+2)2 -
科目: 来源: 题型:
查看答案和解析>>【题目】若a>c,则当m_________时,am<cm; 当m_________时,am=cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=-x2+bx+c经过点B(-1,0)和点C(2,3).
(1)求此抛物线的函数表达式;
(2)如果此抛物线上下平移后过点(-2,-1),请直接写出平移的方向和平移的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:由面积都是1的小正方格组成的方格平面叫做格点平面.而纵横两组平行线的交点叫做格点.如图1中,有9个格点,如果一个正方形的每个顶点都在格点上,那么这个正方形称为格点正方形.
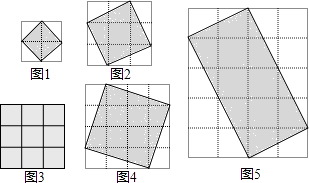
(1)探索发现:按照图形完成下表:格点正方形边上格点数p
格点正方形内格点数q
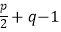
格点正方形面积S
图1
4
1
2
图2
4
4
图3
4
9
图4
4
关于格点正方形的面积S,从上述表格中你发现了什么规律?
(2)继续猜想:类比格点正方形的概念,如果一个长方形的每个顶点都在格点上,那么这个长方形称为格点长方形,对于格点长方形的面积,你认为也有类似(1)中的规律吗?试以图5中格点长方形为例来说明.
相关试题

