【题目】如图,在四边形![]() 中,
中,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,那么下列条件中不能判定四边形
,那么下列条件中不能判定四边形![]() 是菱形的为( )
是菱形的为( )
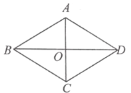
A. ∠OAB=∠OBAB. ∠OBA=∠OBCC. AD∥BCD. AD=BC
参考答案:
【答案】A
【解析】
根据菱形的判定方法有三种:①定义:一组邻边相等的平行四边形是菱形;②四边相等;③对角线互相垂直平分的四边形是菱形,据此判断即可.
A.∵AC⊥BD,BO=DO,
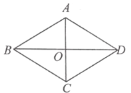
∴AC是BD的垂直平分线,
∴AB=AD,CD=BC,
∴∠ABD=∠ADB,∠CBD=∠CDB,
∵∠OAB=∠OBA,
∴∠OAB=∠OBA=45°,
∵OC与OA的关系不确定,
∴无法证明四边形ABCD的形状,故此选项正确;
B. ∵AC⊥BD,BO=DO,
∴AC是BD的垂直平分线,
∴AB=AD,CD=BC,
∴∠ABD=∠ADA,∠CBD=∠CDB,
∵∠OBA=∠OBC,
∴∠ABD=∠ADB=∠CBD=∠CDB,
BD=BD,
∴△ABD≌△CBD,
∴AB=BC=AD=CD,
∴四边形ABCD是菱形,故此选项错误;
C. ∵AD∥BC,
∴∠DAC=∠ACB,
∵∠AOD=∠BOC,BO=DO,
∴△AOD≌△BOC,
∴AB=BC=CD=AD,
∴四边形ABCD是菱形,故此选项错误;
D. ∵AD=BC,BO=DO,
∠BOC=∠AOD=90°,
∴△AOD≌△BOC,
∴AB=BC=CD=AD,
∴四边形ABCD是菱形,故此选项错误.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某医药研究所开发一种新药,如果成人按规定的剂量服用,据监测:服药后每毫升血液中含药量y与时间t之间近似满足如图所示曲线:
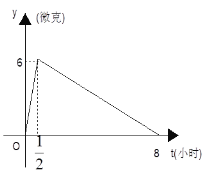
(1)分别求出
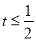 和
和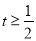 时,y与t之间的函数关系式;
时,y与t之间的函数关系式;(2)据测定:每毫升血液中含药量不少于4微克时治疗疾病有效,假如某病人一天中第一次服药为7:00,那么服药后几点到几点有效?
-
科目: 来源: 题型:
查看答案和解析>>【题目】十一黄金周某一天,甲、乙两名学生去距家36千米的风景区游玩,他们从家出发,骑电动车行驶20分钟时发现忘带相机,甲下车步行前往,乙骑电动车按原路返回,乙取到相机后(在家取相机所用时间忽略不计),骑电动车追甲,在距风景区13.5千米处追上甲并同车前往风景区,若电动车速度始终不变.设甲与家相距
 (千米),乙与家相距
(千米),乙与家相距 (千米),甲离开家的时间为
(千米),甲离开家的时间为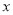 (分钟),
(分钟), 、
、 与x之间的函数图象如图所示,结合图象解答下列问题:
与x之间的函数图象如图所示,结合图象解答下列问题:
(1)求电动车的速度;
(2)求出甲步行的时间是多少分钟?;
(3)求乙返回到家时,甲与家相距多远?
-
科目: 来源: 题型:
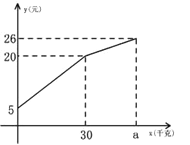
查看答案和解析>>【题目】一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.
(1)农民自带的零钱是多少?
(2)试求降价前y与x之间的关系式
(3)由表达式你能求出降价前每千克的土豆价格是多少?
(4)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
-
科目: 来源: 题型:
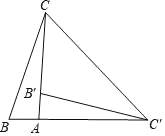
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到的△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B=__________.
-
科目: 来源: 题型:
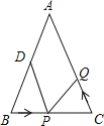
查看答案和解析>>【题目】如图,已知△ABC中,∠B=∠C,BC=8cm,BD=6cm如果点P在线段BC上以1cm/s的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动,当一个点停止运动时,另一个点也随之停止运动,设点Q的速度为xcm/s,则当△BPD与△CQP全等时,x=______.
-
科目: 来源: 题型:
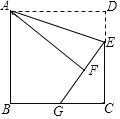
查看答案和解析>>【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且DE=2.将△ADE沿AE对折得到△AFE,延长EF交边BC于点G,则BG=___________.
相关试题

