【题目】在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为![]() 、
、![]() (km),
(km),![]() 、
、![]() 与x的函数关系如图所示.
与x的函数关系如图所示.
(1)填空:A.C两港口间的距离为 km, ![]() ;
;
(2)求图中点P的坐标;
(3)何时甲、乙两船相距18km.

参考答案:
【答案】(1)120, 2;(2)(1,30);(3)![]() 或
或![]() 或
或![]()
【解析】试题分析:(1)从图中可以看出A、B两港是30km,B、C两港是90km,A、C两港口间的距离为30+90=120km,求出甲的速度,进而求出a的值;
(2)求出y1=60x﹣30,y2=30x,解出两个函数的交点,就是点P的坐标.
(3)先根据一次函数的图象求出甲及乙的速度,再根据甲在乙船前和乙船后,及甲船已经到了而乙船正在行驶,三种情况进行解答即可.
试题解析:解:(1)从图中可以看出A、B两港是30km,B、C两港是90km,∴A、C两港口间的距离为30+90=120km,甲的速度为:30÷0.5=60,a=120÷60=2.故答案为:120,2.
(2)由点(3,90)求得,y2=30x,当x≥0.5时,由点(0.5,0),(2,90)求得,y1=60x﹣30,当y1=y2时,60x﹣30=30x,解得x=1,此时y1=y2=30,∴点P的坐标是(1,30).
(3)甲的速度为每小时60千米,乙的速度为每小时30千米,设x小时相距18千米,分三种情况讨论:
①第一种情况:60x﹣30x=30﹣18,解得x=![]() ;
;
②第二种情况:60x﹣30x=30+18,解得,x=![]() ;
;
③第三种情况,甲船停靠C港后,乙船继续航行,当乙船行72千米时,与甲船也相距18千米,所以时间为:72÷30=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校“综合实践课程”结合当地传统文化开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如下不完整分布表及条形统计图 .

根据以上信息完成下列问题:
(1)直接写出分布表中a的值;
(2)补全条形统计图;
(3)若全校共有学生1000名,估计该校最喜爱围棋的学生大约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,点P的坐标为(a+1,a﹣1).
(1)试判断点P是否在一次函数y=x﹣2的图象上,并说明理由;
(2)如图,一次函数
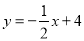 的图象与x轴、y轴分别相交于点A、B,若点P在△AOB的内部,求a的取值范围.
的图象与x轴、y轴分别相交于点A、B,若点P在△AOB的内部,求a的取值范围.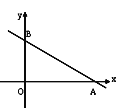
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(x﹣1)(x+2)的结果是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】4的平方根是( )
A. 2 B. ﹣2 C. ±2 D. ±4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=-2x+2的图像与x轴、y轴分别交于A、B两点.
(1)求图像与坐标轴围成的图形的面积.
(2)过C(0,1)作CD⊥AB于点P,交x轴于点D,求直线CD的解析式.
(3)点M从点D出发,以每秒1个单位长度的速度沿x轴向右运动,设运动时间为t(秒),△APM的面积为S.
①求出S关于t的函数关系式;
②运动多少秒时,△APD被PM分成的两部分面积比为1:5;
③连接AC,Q为直线AB上一点,当OQ垂直平分线段AC时,OQ把△AOB分成的两部分面积比为多少.(请直接写出答案)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD是∠BAC的平分线,AE是∠BAC的外角平分线,ED∥AB交AC于点G.下列结论:①AD⊥AE;②AE∥BC;③AE=AG;④AG=
 DE.正确的是________.(填序号)
DE.正确的是________.(填序号) 
相关试题

