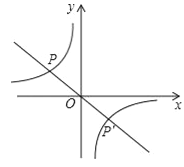
【题目】如图,点P(﹣3,1)是反比例函数![]() 的图象上的一点.
的图象上的一点.
(1)求该反比例函数的解析式;
(2)设直线y=kx与双曲线![]() 的两个交点分别为P和P′,当
的两个交点分别为P和P′,当![]() <kx时,直接写出x的取值范围.
<kx时,直接写出x的取值范围.
参考答案:
【答案】(1)![]() ;(2)x<﹣3或0<x<3.
;(2)x<﹣3或0<x<3.
【解析】
试题分析:(1)直接把P点坐标代入y=![]() ,可求出m的值.从而确定反比例函数的解析式;
,可求出m的值.从而确定反比例函数的解析式;
(2)把P(﹣3,1)坐标代入y=kx,求出k,然后解反比例函数与一次函数的解析式所组成的方程组得到P′的坐标(3,﹣1),然后观察图象得到当x<﹣3或0<x<3,直线y=kx都在y=![]() 的上方.
的上方.
试题解析:(1)把P(﹣3,1)代入y=![]() 得m=﹣3×1=﹣3,所以反比例函数的解析式为
得m=﹣3×1=﹣3,所以反比例函数的解析式为![]() ;
;
(2)把P(﹣3,1)代入y=kx得![]() ,∴
,∴![]() ,解方程组
,解方程组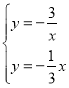 ,得
,得![]() 或
或![]() ,∴P′的坐标为(3,﹣1),当
,∴P′的坐标为(3,﹣1),当![]() <kx时,x的取值范围为x<﹣3或0<x<3.
<kx时,x的取值范围为x<﹣3或0<x<3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题:探索发现
(1)分解因式:①(1+x)+x(1+x)=()()=()2
②(1+x)+x(1+x) + x(1+x)2=
③(1+x)+x(1+x) + x(1+x)2 + x(1+x)3=
(2)根据(1)的规律,直接写出多项式:(1+x) +x(1+x) + x(1+x)2+…+ x(1+x)2017分解因式的结果:。
(3)变式: = .
= . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:A(0,4),点C在y轴上,AC=5,则点C的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E在直线BH、DC之间,点A为BH上一点,且AE⊥CE,
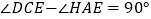 .
.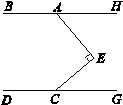
(1)求证:BH∥CD;
(2)如图:直线AF交DC于F,AM平分∠EAF,AN平分∠BAE. 试探究∠MAN,∠AFG的数量关系.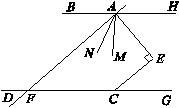
-
科目: 来源: 题型:
查看答案和解析>>【题目】若m,n是方程x2+2015x﹣1=0的两个实数根,则m2n+mn2﹣mn的值等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F.
(1)求证:EF是⊙O的切线;
(2)若EB=
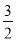 ,且sin∠CFD=
,且sin∠CFD= ,求⊙O的半径与线段AE的长.
,求⊙O的半径与线段AE的长.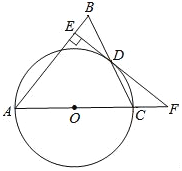
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前节能灯在城市已基本普及,今年山东省面向县级及农村地区推广节能灯,为响应号召,某商场计划购进甲、乙两种节能灯共1200只,这两种节能灯的进价、售价如下表:
进价(元/只)
售价(元/只)
甲
25
30
乙
45
60
(1)如何进货,进货款恰好为46000元?
(2)如何进货,商场销售完节能灯时获利最多且不超过进货价的30%,此时利润为多少元?
相关试题

