搜索
【题目】如图，点E在直线BH、DC之间，点A为BH上一点，且AE⊥CE， 
.
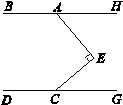
（1）求证：BH∥CD；
（2）如图：直线AF交DC于F，AM平分∠EAF，AN平分∠BAE. 试探究∠MAN，∠AFG的数量关系.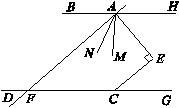
参考答案：
【答案】
（1）解：延长AE交DC于点F
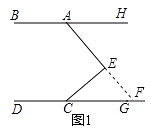
∵∠DCE=∠EFC+90°， 
∴∠HAE=∠EFC
∴BH∥CD；
（2）解：∵BH∥CD
∴∠BAF=∠AFG
∵AM平分∠EAF，AN平分∠BAE
∴∠MAN＝∠EAN-∠EAM= 
（∠BAE-∠EAF）= ∠BAF
∴∠MAN＝ ∠AFG
【解析】（1）通过延长构造出第三条直线，进而构造出内错角，利用外角定理证出内错角相等，进而证出平行；（2）利用平行线的性质和平分线的定义可证出结论.
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲，乙两支仪仗队队员的身高（单位：cm）如下：
甲队：178，177，179，178，177，178，177，179，178，179；
乙队：178，179，176，178，180，178，176，178，177，180；
（1）将下表填完整：身高
176
177
178
179
180
甲队（人数）
3
4
乙队（人数）
2
1
1
（2）甲队队员身高的平均数为cm，乙队队员身高的平均数为cm；
（3）你认为哪支仪仗队更为整齐？简要说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】综合题:探索发现
（1）分解因式：①（1＋x）＋x(1＋x)＝（）（）＝（）2
②（1＋x）＋x(1＋x) ＋ x(1＋x)2＝
③（1＋x）＋x(1＋x) ＋ x(1＋x)2 ＋ x(1＋x)3＝
（2）根据（1）的规律，直接写出多项式：(1＋x) ＋x(1＋x) ＋ x(1＋x)2＋…＋ x(1＋x)2017分解因式的结果：。
（3）变式：
= . -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：A（0，4），点C在y轴上，AC=5，则点C的坐标为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点P（﹣3，1）是反比例函数
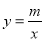的图象上的一点．（1）求该反比例函数的解析式；
（2）设直线y=kx与双曲线
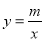的两个交点分别为P和P′，当
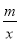＜kx时，直接写出x的取值范围．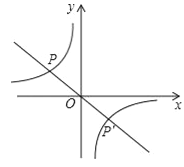
-
科目： 来源： 题型：
查看答案和解析>>【题目】若m，n是方程x2+2015x﹣1=0的两个实数根，则m2n+mn2﹣mn的值等于 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，以AC边为直径作⊙O交BC边于点D，过点D作DE⊥AB于点E，ED、AC的延长线交于点F．
（1）求证：EF是⊙O的切线；
（2）若EB=
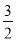，且sin∠CFD=
，求⊙O的半径与线段AE的长．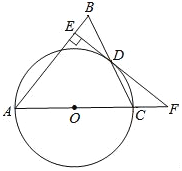
相关试题
