Question

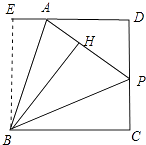
【题目】如图，已知四边形ABCD中，AD∥BC，∠C=90°，P是CD上一点，BH⊥AP于H，BH=BC=CD

（1）求证：∠ABP=45°；
（2）若BC=20，PC=12，求AP的长．

Answer 1

【答案】
（1）证明：如图，作BE⊥DA于E，

∵AD∥BC，∠C=90°，

∴∠C+∠D=180°，

∴∠D=∠C=∠E=90°，

∴四边形BCDE是矩形，

∴BE=CD=BC=BH，

∵BH⊥AP，

∴∠AHB=∠BHP=90°，

在Rt△ABE和Rt△ABH中，

，

∴△ABE≌△ABH，

∴∠ABE=∠ABH，同理可证△PBH≌△PBC，

∴∠PBH=∠PBC，

∵∠EBC=90°，

∴2∠ABH+2∠PBH=90°，

∴∠ABH+∠PBH=45°，

∴∠ABP=45°

（2）证明：由（1）可知，四边形BCDE是矩形，

∵BC=CD，

∴四边形BCDE是正方形，

∴BC=CD=DE=BE=20，

∵△ABE≌△ABH，△PBH≌△PBC，

∴AE=AH，PC=PH，

∴AP=AE+PC，设AP=x，

则AE=x﹣12，AD=20﹣（x﹣12）=32﹣x，PD=8，

在Rt△ADP中，∵AD2+DP2=AP2，

∴（32﹣x）2+82=x2，

∴x=17，

∴AP=17．

【解析】（1）如图，作BE⊥DA于E，只要证明△ABE≌△ABH，△PBH≌△PBC，推出∠ABE=∠ABH，∠PBH=∠PBC，由∠EBC=90°，推出2∠ABH+2∠PBH=90°，由此即可证明．（2）首先证明AP=AE+PC，设PA=x，在Rt△ADP中，利用勾股定理列出方程即可解决问题．