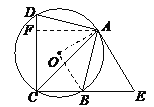
【题目】如图,已知四边形ABCD内接于⊙O,点E在CB的延长线上,连结AC、AE,∠ACB=∠BAE=45°.
(1)求证:AE是⊙O的切线;
(2)若AB=AD,AC=![]() ,tan∠ADC=3,求BE的长.
,tan∠ADC=3,求BE的长.

参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)连接OA、OB,由圆周角定理得出∠AOB=2∠ACB=90°,由等腰直角三角形的性质得出∠OAB=∠OBA=45°,求出∠OAE=∠OAB+∠BAE=90°,即可得出结论;(2)过点A作AF⊥CD于点F,由AB=AD,得到∠ACD=∠ACB=45°,在Rt△AFC中可求得AF=3,在Rt△AFD中求得DF=1,所以AB=![]() =
=![]() ,CD= CF+DF=4,再证明△ABE∽△CDA,得出
,CD= CF+DF=4,再证明△ABE∽△CDA,得出![]() ,即可求出BE的长度;
,即可求出BE的长度;
试题解析:
(1)证明:连结OA,OB,
∵∠ACB=45°,
∴∠AOB=2∠ACB= 90°,
∵OA=OB,
∴∠OAB=∠OBA=45°,
∵∠BAE=45°,
∴∠OAE=∠OAB+∠BAE=90°,
∴OA⊥AE.
∵点A在⊙O上,
∴AE是⊙O的切线.
(2)解:过点A作AF⊥CD于点F,则∠AFC=∠AFD=90°.
∵AB=AD,
∴![]() =
=![]()
∴∠ACD=∠ACB=45°,
在Rt△AFC中,
∵AC=![]() ,∠ACF=45°,
,∠ACF=45°,
∴AF=CF=AC·sin∠ACF =3,
∵在Rt△AFD中, tan∠ADC=![]() ,
,
∴DF=1,
∴![]() ,
,
且CD= CF+DF=4,
∵四边形ABCD内接于⊙O,
∴∠ABE=∠CDA,
∵∠BAE=∠DCA,
∴△ABE∽△CDA,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF,BC=5,CF=3,BF=4.求证:DE∥FC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一名老师带领x名学生到动物园参观,已知成人票每张30元,学生票每张10元.设门票的总费用为y元,则y与x的函数关系为( )
A. y=10x+30 B. y=40x C. y=10+30x D. y=20x
-
科目: 来源: 题型:
查看答案和解析>>【题目】规定:符号“&”为选择两数中较大数的运算,“◎”为选择两数中较小数的运算,则(4◎3)×(2&5)的结果为__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠CAB=50°,按以下步骤作图:

①以点A为圆心,小于AC长为半径画弧,分别交AB、AC于点E、F;
②分别以点E、F为圆心,大于 EF长为半径画弧,两弧相交于点G;
EF长为半径画弧,两弧相交于点G;
③作射线AG , 交BC边于点D .
则∠ADC的度数为( )
A.40°
B.55°
C.65°
D.75° -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各式:
13=12
13+23=32
13+23+33=62
13+23+33+43=102
…
猜想13+23+33+…+103= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD中,AD∥BC,∠C=90°,P是CD上一点,BH⊥AP于H,BH=BC=CD

(1)求证:∠ABP=45°;
(2)若BC=20,PC=12,求AP的长.
相关试题

