【题目】实践与探索:将连续的奇数 1,3,5,7…排列成如下的数表,用十字框框出 5 个数(如图)
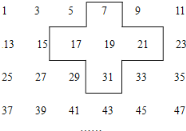
(1)若将十字框上下左右平移,但一定要框住数列中的 5 个数,若设中间的数为 a,用 a 的代数式表示十字框框住的 5 个数字之和;
(2)十字框框住的 5 个数之和能等于 285 吗?若能,分别写出十字框框住的 5 个数;若不能,请说明理由;
(3)十字框框住的 5 个数之和能等于 365 吗?若能,分别写出十字框框住的 5 个数;若不能,请说明理由.
参考答案:
【答案】(1) 5a;⑵可以;45,55,57,59,69;⑶不可能.
【解析】
(1)从表格可看出上下相邻相差12,左右相邻相差2,中间的数为a,上面的为a-12,下面的为a+12,左面的为a-2,右面的为a+2,这5个数的和可用a来表示,
(2)代入285看看求出的结果是整数就可以,再考虑中间数的位置,即可得出答案.
(3)代入365看看求出的结果是整数就可以,再考虑中间数的位置,即可得出答案.
解:(1)从表格知道中间的数为 a,上面的为 a-12,下面的为 a+12,左面的为 a-2,右面的为 a+2, a+(a-2)+(a+2)+(a-12)+(a+12)=5a;
⑵5a=285,a=57,a=57 为奇数在第 5 列,所以可以,
十字框框住的 5 个数分别,45,55,57,59,69;.
⑶5a=365, a=73,
又因为 73÷12=6.....1,所以 73 在第 7 行第一列,
因为我们设的 a 是十字框正中间的数,故不可能.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
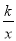 ,当x=-
,当x=-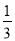 时,y=-6.
时,y=-6.(1)这个函数的图象位于哪些象限?y随x的增大如何变化?
(2)当
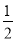 <x<4时,求y的取值范围.
<x<4时,求y的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+5(k为常数,且k≠0)的图象与反比例函数y=-
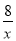 的图象交于A(-2,b),B两点.
的图象交于A(-2,b),B两点.(1)求一次函数的表达式;
(2)若将直线AB向下平移m(m>0)个单位长度后,与反比例函数的图象有且只有一个公共点,求m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,P是对角线AC上一点(不与点A、C重合),连接PD,过点P作PE⊥PD交射线BC于点E.
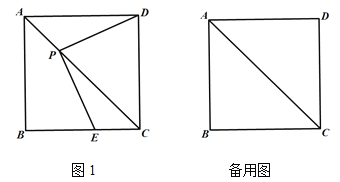
(1)如图1,求证:PD=PE;
(2)若正方形ABCD的边长为4,
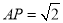 ,求CE长.
,求CE长. -
科目: 来源: 题型:
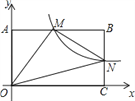
查看答案和解析>>【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在坐标轴上,点B的坐标为(4,2),直线y=–
 x+3交AB,BC于点M,N,反比例函数
x+3交AB,BC于点M,N,反比例函数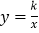 的图象经过点M,N.
的图象经过点M,N.(1)求反比例函数的解析式;
(2)若点P在x轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )
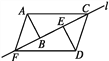
A. 四边形ACDF是平行四边形 B. 当点E为BC中点时,四边形ACDF是矩形
C. 当点B与点E重合时,四边形ACDF是菱形 D. 四边形ACDF不可能是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】学习过绝对值之后,我们知道:|5-2|表示 5 与 2 的差的绝对值,实际上也可理解为 5 与 2 两数在数轴上所对应的两点之间的距离:|5+2|表示 5 与-2 的差的绝对值,实际上也可理解为 5 与-2 两数在数轴上所对应的两点之间的距离. 试探究解决以下问题:
⑴|x+6|可以理解为 与 两数在数轴上所对应的两点之间的距离;
⑵找出所有符合条件的整数 x,使|x+1|+|x-2|=3 成立;
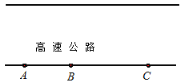
⑶如图,在一条笔直的高速公路旁边依次有 A、B、C 三个城市,它们距高速公路起点的距离分别是 567km、689km、889km.现在需要在该公路旁建一个物流集散中心 P,请直接指出该物流集散中心 P 应该建设在何处,才能使得 P 到三个城市的距离之和最小?这个最小距离是多少?
相关试题

