【题目】如图,在正方形ABCD中,P是对角线AC上一点(不与点A、C重合),连接PD,过点P作PE⊥PD交射线BC于点E.
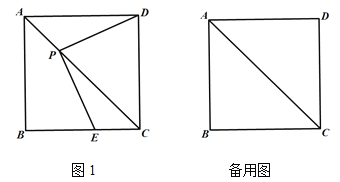
(1)如图1,求证:PD=PE;
(2)若正方形ABCD的边长为4,![]() ,求CE长.
,求CE长.
参考答案:
【答案】(1)证明见解析;(2)2.
【解析】
(1)如图1中,连接PB,利用△APB≌△APD推出PB=PD,再证明PB=PE即可解决问题.
(2)可通过构建等腰直角三角形来求解.过点P作GF∥AB,分别交AD、BC于G、F,那么△AGP和△PFC都是等腰直角三角形,四边形ABFG和四边形GFCD都是矩形,可得AG=BF=PG=1.而PB=PE,PF⊥BE,那么根据等腰三角形三线合一的特点可得出BF=FE=AG=PG,从而CE=BC-2AG=4-2=2.
1)如图1中,连接PB.
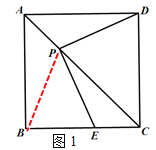
∵四边形ABCD是正方形,
∴AB=AD,∠BAC=∠DAC=45°,∠ABC=∠ADC=∠BCD=90°
在△APB和△APD中,
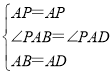 ,
,
∴△APB≌△APD,
∴PB=PD,∠ADP=∠ABP,
∴∠PBC=∠PDC,
∵∠DPE=∠BCD=90°,
∴∠PEC+∠PDC=180°,∠PEB+∠PEC=180°,
∴∠PEB=∠PDC,
∴∠PBC=∠PEB,
∴PB=PE,
∴PD=PE.
(2)过点P作GF∥AB,分别交AD、BC于G、F.如图所示.
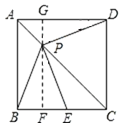
∵四边形ABCD是正方形,
∴四边形ABFG和四边形GFCD都是矩形,
△AGP和△PFC都是等腰直角三角形.
又∵AP=![]() ,AD=4,
,AD=4,
∴GP=AG=BF=1,GD=FC=FP=41=3,
又∵PB=PE,PF⊥BE
∴BF=FE,
∴CE=4-2=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】蜗牛从某点O开始沿东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬行的各段路程依次为(单位:厘米):
 .问:
.问:(1)蜗牛最后是否回到出发点O?
(2)蜗牛离开出发点O最远是多少厘米?
(3)在爬行过程中,如果每爬行1厘米奖励一粒芝麻,则蜗牛可得到多少粒芝麻?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
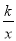 ,当x=-
,当x=-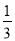 时,y=-6.
时,y=-6.(1)这个函数的图象位于哪些象限?y随x的增大如何变化?
(2)当
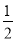 <x<4时,求y的取值范围.
<x<4时,求y的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+5(k为常数,且k≠0)的图象与反比例函数y=-
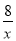 的图象交于A(-2,b),B两点.
的图象交于A(-2,b),B两点.(1)求一次函数的表达式;
(2)若将直线AB向下平移m(m>0)个单位长度后,与反比例函数的图象有且只有一个公共点,求m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】实践与探索:将连续的奇数 1,3,5,7…排列成如下的数表,用十字框框出 5 个数(如图)
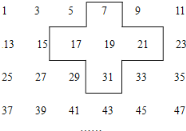
(1)若将十字框上下左右平移,但一定要框住数列中的 5 个数,若设中间的数为 a,用 a 的代数式表示十字框框住的 5 个数字之和;
(2)十字框框住的 5 个数之和能等于 285 吗?若能,分别写出十字框框住的 5 个数;若不能,请说明理由;
(3)十字框框住的 5 个数之和能等于 365 吗?若能,分别写出十字框框住的 5 个数;若不能,请说明理由.
-
科目: 来源: 题型:
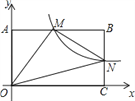
查看答案和解析>>【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在坐标轴上,点B的坐标为(4,2),直线y=–
 x+3交AB,BC于点M,N,反比例函数
x+3交AB,BC于点M,N,反比例函数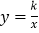 的图象经过点M,N.
的图象经过点M,N.(1)求反比例函数的解析式;
(2)若点P在x轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )
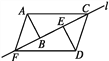
A. 四边形ACDF是平行四边形 B. 当点E为BC中点时,四边形ACDF是矩形
C. 当点B与点E重合时,四边形ACDF是菱形 D. 四边形ACDF不可能是正方形
相关试题

