【题目】学习过绝对值之后,我们知道:|5-2|表示 5 与 2 的差的绝对值,实际上也可理解为 5 与 2 两数在数轴上所对应的两点之间的距离:|5+2|表示 5 与-2 的差的绝对值,实际上也可理解为 5 与-2 两数在数轴上所对应的两点之间的距离. 试探究解决以下问题:
⑴|x+6|可以理解为 与 两数在数轴上所对应的两点之间的距离;
⑵找出所有符合条件的整数 x,使|x+1|+|x-2|=3 成立;
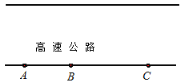
⑶如图,在一条笔直的高速公路旁边依次有 A、B、C 三个城市,它们距高速公路起点的距离分别是 567km、689km、889km.现在需要在该公路旁建一个物流集散中心 P,请直接指出该物流集散中心 P 应该建设在何处,才能使得 P 到三个城市的距离之和最小?这个最小距离是多少?
参考答案:
【答案】⑴x 与-6;⑵-1、0、1、2;⑶应该建在 B 处,相距 322 km.
【解析】
(1)|x+6|表示 x 与-6 的差的绝对值,即可求解;
(2)|x+1|+|x-2|表示数轴上有理数x所对应的点到-1和2所对应的点的距离之和,而-1到2的距离等于3, 所以x所对应的点在-1和2之间,含-1和2,即可求解;
(3)以高速公路起点为数轴原点建立数轴,点P应在A、C之间,此时PA+PC=|889-567|=322,所以当PB=0,PA+PB+PC最小.
解:⑴|x+6|可以理解为x与-6两数在数轴上所对应的两点之间的距离;
(2)∵|x+1|+|x-2|表示数轴上有理数x所对应的点到-1和2所对应的点的距离之和,而-1到2的距离等于3,|x+1|+|x-2|=3,
∴x所对应的点在-1和2之间,含-1和2
∴这样的整数有-1、0、1、2.
故答案为:-1、0、1、2.
(3)如图,以高速公路起点为数轴原点建立数轴
![]()
则A、B、C 三个城市在数轴上表示的数分别是567、689、889,
设点P表示的数为x,则
PA+PB+PC=|x-567|+|x-689|+|x-889|,
显然,点P应在A、C之间,此时PA+PC=|889-567|=322,
所以当PB最小时,PA+PB+PC最小,
即当点P在B点时,PB=0,PA+PB+PC最小,等于322 km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】实践与探索:将连续的奇数 1,3,5,7…排列成如下的数表,用十字框框出 5 个数(如图)
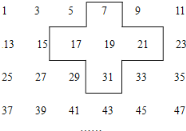
(1)若将十字框上下左右平移,但一定要框住数列中的 5 个数,若设中间的数为 a,用 a 的代数式表示十字框框住的 5 个数字之和;
(2)十字框框住的 5 个数之和能等于 285 吗?若能,分别写出十字框框住的 5 个数;若不能,请说明理由;
(3)十字框框住的 5 个数之和能等于 365 吗?若能,分别写出十字框框住的 5 个数;若不能,请说明理由.
-
科目: 来源: 题型:
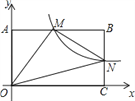
查看答案和解析>>【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在坐标轴上,点B的坐标为(4,2),直线y=–
 x+3交AB,BC于点M,N,反比例函数
x+3交AB,BC于点M,N,反比例函数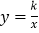 的图象经过点M,N.
的图象经过点M,N.(1)求反比例函数的解析式;
(2)若点P在x轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )
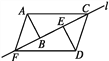
A. 四边形ACDF是平行四边形 B. 当点E为BC中点时,四边形ACDF是矩形
C. 当点B与点E重合时,四边形ACDF是菱形 D. 四边形ACDF不可能是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为【 】

A.1 B.
 C. 2 D.
C. 2 D. +1
+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,BC=2AB,对角线相交于O,过C点作CE⊥BD交BD于E点,H为BC中点,连接AH交BD于G点,交EC的延长线于F点,下列5个结论:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④S△GAD=S四边形GHCE;⑤CF=BD.正确的有( )个.
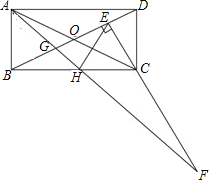
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
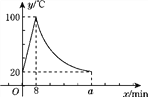
查看答案和解析>>【题目】教师办公室有一种可以自动加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10 ℃,待加热到100 ℃,饮水机自动停止加热,水温开始下降,水温y(℃)和通电时间x(min)成反比例函数关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温均为20 ℃,接通电源后,水温y(℃)和通电时间x(min)之间的关系如图所示,回答下列问题:
(1)分别求出当0≤x≤8和8<x≤a时,y和x之间的函数关系式;
(2)求出图中a的值;
(3)李老师这天早上7:30将饮水机电源打开,若他想在8:10上课前喝到不低于40 ℃的开水,则他需要在什么时间段内接水?
相关试题

